A number theory problem by Naren Bhandari

Number Theory Level 1

If N ! = S \large \color{#3D99F6}{N!} = \color{#D61F06}{S}

Here S \color{#D61F06}{S} carries total number of seconds in six weeks. Find N \color{#3D99F6}{N} .


Notation: ! ! is the factorial notation. For example, 8 ! = 1 × 2 × 3 × ⋯ × 8 8! = 1\times2\times3\times\cdots\times8 .

6 7 9 10

Naren Bhandari by Naren Bhandari , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Adam Hufstetler
Mar 21, 2017

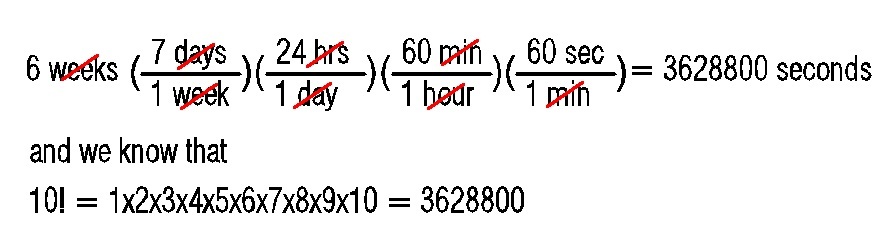
The number of seconds in six weeks is
60 ⋅ 60 ⋅ 24 ⋅ 7 ⋅ 6 60\cdot60\cdot24\cdot7\cdot6 or ( 2 2 ⋅ 3 ⋅ 5 ) ( 2 2 ⋅ 3 ⋅ 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) (2^2\cdot3\cdot5)(2^2\cdot3\cdot5)(2^3\cdot3)(7)(2\cdot3)
Let's attempt to reorganize these numbers in a form of N ! N! starting from 1 1 :
N ! = 1 ! ⋅ ( 2 2 ⋅ 3 ⋅ 5 ) ( 2 2 ⋅ 3 ⋅ 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) N!=1!\cdot(2^2\cdot3\cdot5)(2^2\cdot3\cdot5)(2^3\cdot3)(7)(2\cdot3)
= 2 ! ⋅ ( 2 ⋅ 3 ⋅ 5 ) ( 2 2 ⋅ 3 ⋅ 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) =2!\cdot(2\cdot3\cdot5)(2^2\cdot3\cdot5)(2^3\cdot3)(7)(2\cdot3)
= 3 ! ⋅ ( 2 ⋅ 5 ) ( 2 2 ⋅ 3 ⋅ 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) =3!\cdot(2\cdot5)(2^2\cdot3\cdot5)(2^3\cdot3)(7)(2\cdot3)
= 4 ! ⋅ ( 2 ⋅ 5 ) ( 3 ⋅ 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) =4!\cdot(2\cdot5)(3\cdot5)(2^3\cdot3)(7)(2\cdot3)
= 5 ! ⋅ ( 2 ) ( 3 ⋅ 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) =5!\cdot(2)(3\cdot5)(2^3\cdot3)(7)(2\cdot3)
= 6 ! ⋅ ( 5 ) ( 2 3 ⋅ 3 ) ( 7 ) ( 2 ⋅ 3 ) =6!\cdot(5)(2^3\cdot3)(7)(2\cdot3)
= 7 ! ⋅ ( 5 ) ( 2 3 ⋅ 3 ) ( 2 ⋅ 3 ) =7!\cdot(5)(2^3\cdot3)(2\cdot3)
= 8 ! ⋅ ( 5 ) ( 3 ) ( 2 ⋅ 3 ) =8!\cdot(5)(3)(2\cdot3)
= 9 ! ⋅ ( 5 ) ( 2 ) =9!\cdot(5)(2)
N ! = 10 ! N!=10!
N = 10 N=10

Side Note: Does anyone know how to insert a tab to line the = = 's up?

17 Helpful 0 Interesting 0 Brilliant 0 Confused

Use the Latex expression

\begin{align} N! &= ..... \

&=..... \

.

.

&=...... \end{align}

The \align command helps you to adjust your input into column-like arrangements with the help of the '&' function.

Tapas Mazumdar - 4 years, 2 months ago
Lohith Tummala
Mar 31, 2017

Knowing that there are 3600 seconds in an hour, and 10! is the only option with two trailing zeroes, that must be our answer.

6 Helpful 0 Interesting 1 Brilliant 0 Confused

In 6 6 weeks there are,

4 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...