Angles In A 7-Pointed Star
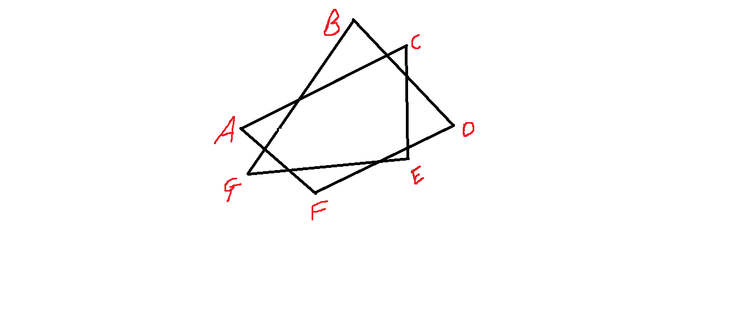 If all line segments are straight in the given figure, then sum of the angles at the corners marked in the diagram (in degrees) is
If all line segments are straight in the given figure, then sum of the angles at the corners marked in the diagram (in degrees) is
The answer is 540.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
It's not a heptagon; it's a fourteen-gon.
i made it 1260 - 720 = 360. 2 times and i gave up. lol
i thought 630 :(
shoter way
x= inter angle of heptagon adjacent to <int1 y= inter angle of heptagon adjacent to int<2
-
analyze only one triangle (preferably at A)
-
x = -180 +<int1 ; y = -180 + <int 2
-
<A = 180 - <int1 - <int 2 = 180 - (-180 +<int 1) - (-180 + <int 2)
-
<A = 3(180) + <int 1 + <int 2 ; analyze
-
sum(corner angles) = (n +1)180 - sum(int angles)
-
sum(corner angles) = (7+1)180 - (n-2)180 = 1440 - 900 = 540....check
I didn't understand triangle part where you excluded them.
Fastest method:- outer triangles = 180x7 | sum of exterior angles = 360x2 =180x4| difference = 180x(7-4) = 180x3 = 540
= 180(n-4)=3 * 180=540 (you can use this to prove that the least number of angels of a star is five)
Sum of the 7 interior angle of the heptagon = (7-2) 180 = 900 Value of one interior angle = 900/7 = 128.6 Value of one exterior angle of the heptagon = 180 - 128.6 = 51.4 Corner angle = 180 - 51.4 2 = 77.14 Sum of 7 corner angle = 7*77.14 = 540 degrees
how is 180-51.42=77.14 in your solution??
a + c + g +e = 360 -x b+d +f=180 +x
Adding the above solves it. x is the interior angle of triangle with vetrex G and triangle with vertex A (oppsite angles)
i did the same way
i too solved in this way
Try to see seven triangles and a heptagon. The sum of the external angles of the seven triangles is 6300 (900 each). The sum of the internal angles of the heptagon is 900. The external angle of the corners (A - G) is nothing more then 360 - the corner internal angle, and the sum of the external angles of the other corners of the seven triangles is nothing more then 360 * 7 + 2 * Sum of the internal angles of the heptagon (900). That makes an equation:
6300 = 360 * 7 - (A + B + C + D + E + F + G) + 360 * 7 + 2 * 900
6300 = 360 * 14 + 1800 - ( A + B + C + D + E + F + G)
(A + B + C + D + E + F + G) = 540
Assume the picture as a 3D. It would be like a triangle(interior angle sum=180) cut through a quadrilateral (sum of interior angles=360). Hence its 540.
I don't quite understand what you are saying. Can you explain?
Log in to reply
Look like she glanced it as a triangle overlapping a quadrilateral , just like me, so we quickly came up with the answer (540). Must be coincidence that it is correct answer...
@Anitha Raj w0w so easy!! Anitha Raj
formei 7 quadriláteros com 3 ângulos nas letras e uma ângulo no heptágono do interior do desenho. Somei tudo e deu: 900 + 3(A+B+C+D+E+F+G) = 7*360. Logo A+B+C+D+E+F+G= 540 graus
Name the intersection of GB and AC as O..
name all the angles as there corners like ∠ GEC = ∠ E
now ∠ G + ∠ E + ∠ C + ∠ GOC = 360' --------- 1
Now Join BA
∠ B + ∠ A + ∠ F + ∠ D + ∠ OAB + ∠ OBA = 360' ---------------2
∠ GOC = ∠ AOB (v.o.a)
Add eq 1and 2
∠ A+ ∠ B+ ∠ C+ ∠ D+ ∠ E+ ∠ F+ ∠ G + ∠ AOB + ∠ OAB + ∠ OBA = 360' + 360'
∠ AOB + ∠ OAB + ∠ OBA = 180' , as they are angles of triangle)
∠ A+ ∠ B+ ∠ C+ ∠ D+ ∠ E+ ∠ F+ ∠ G = 720' - 180'
∠ A+ ∠ B+ ∠ C+ ∠ D+ ∠ E+ ∠ F+ ∠ G = 540'
Thanks kartik!
Since the specific angles are not specified, assume that this is a regular heptagonal star. The angles of each of the equal angles in the triangles will be 360/7. So the angle of the odd angle out is 180 - 2(360/7). We get:
180 -720/7 1260/7 - 720/7 540/7. And since there are seven of these, our answer for the total is 540.
there are 7 triangle let we have to find the angle A,B,C,D,E,F,G Also, there are triangle APQ,BQR ,CRS ,DST , ETU , FUV ,GVP triangle APQ, angle A = 180 - <1-<2 triangle BQR ,angle B = 180 - <2 - <3 triangle CRS , angle C = 180 - <3- <4 triangle CST , angle D = 180 - <4 - <5 triangle ETU , angle E = 180 - <5 - <6 triangle , FUV , angle F = 180 - <6 - <7 triangle , GVP , angle G = 180 - <7 - <1 SO , angle (A+B+C+D +E+F+G) = 1260 - 2(1+2+3+4+5+6+7) -----------------------------------------------(1) = 1260 - 2(180 -<A + 180 - <C + 180 - <F + <5) = 1260 - 2(540) - 2(angle A+C+F -< 5) = 1260 - 1080 - 2(angle A+C+F - <5) ------------------------------------------(2) also, in quadrilateral , ACTF, angle (A+C+<CTF + F) = 360 angle (A+C)+(180-<5)+ F = 360 angle (A+C+F) - < 5 = 180 ----------------------------------------------------(3) putting, Eqn. (3) into (2) , we get , angle ( A+B+C+D+E+F+G) = 540
since the figure is composed of a triangle and a quadrilateral overlapping each other, therefore, we will just add the total measure of interior angles of a quadrilateral and that of the triangle. For quadrilateral, it is 360 degrees and for triangle is 180 degrees. Now, we can get the answer, 540 degrees.
Log in to reply
How is it a triangle overlapping a quadrilateral? What are the vertices of the triangle and quadrilateral?
Log in to reply
I'm so sorry. . .i wasn't able to look at it closely. .
Look closely, it is not a triangle and a quadrilateral overlapping each other.
corner angle = pi - (pi - adjacent interior angle of inner 7 sided polygon) - (pi - other adjacent interior angle of inner 7 sided polygon).
summation(corner angle) = 2 summation(interior angles) - 7 pi = 15 pi - 7 pi = 3*pi = 540 degrees
Heptagrammic prism (7/2)
the formula is : = 180(p-2q)= 540 ; p=7,q=2
sorry that is 10pi-7pi. 2summation(interior angles)=2 (n-2) pi=2 (7-2) pi=10pi. The first step is on the outermost triangle of the figure containing the corner angle. The second step sums up all these corner angles.
The sum of all of the angles of the 7 triangles on each side of the heptagon is 7 ⋅ 1 8 0 = 1 2 6 0 degrees.
The sum of the exterior angles of the heptagon is 3 6 0 degrees.
The sum of all of the angles of the 7 triangles excluding the angles at the corners is 2 times the sum of the exterior angles (2 sets of exterior angles), which is 2 ⋅ 3 6 0 = 7 2 0 degrees.
The sum of the angles at the corners is 1 2 6 0 − 7 2 0 = 5 4 0 degrees.