An Old Chestnut

Probability Level 3

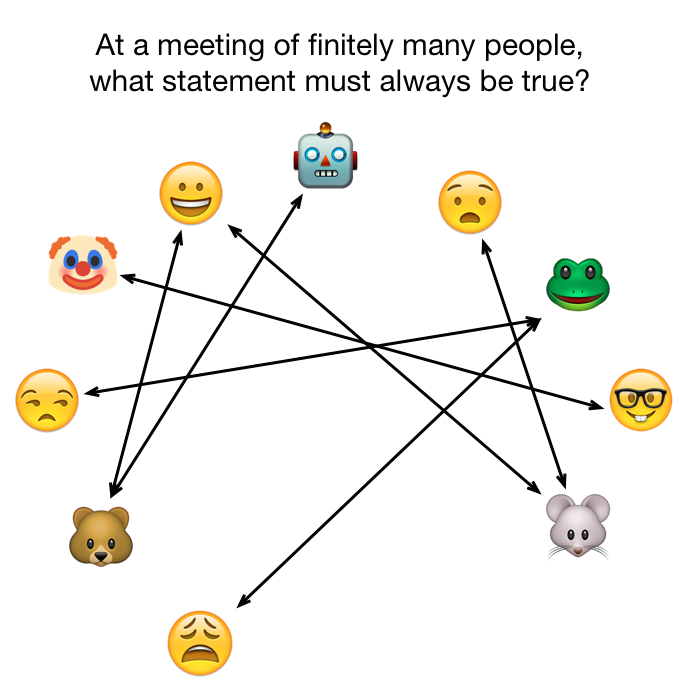
At a meeting with a finite number of attendees, which of the following statements must be true?

An odd number of people shook hands an odd number of times. An even number of people shook hands an even number of times An odd number of people shook hands an even number of times. An even number of people shook hands an odd number of times

Peter Macgregor by Peter Macgregor , 64, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Peter Macgregor
Apr 27, 2016

If two people shake hands, let us say there has been two handshakes,(because both people have shaken hands once). With this understanding the total number of handshakes must be even.

Now imagine asking each attendee how many times they shook hands, and keep a record of the parity of the total. By parity I mean odd or evenness. Before you ask any questions your total is zero, so the parity is even. Since we know that the number of handshakes is even, the final parity must be even. So the parity must change an even number of times as you take your survey of all the attendees.The people who have shaken hands an even number of times do not change the parity and each person who has shaken hands an odd number of times will change the parity. So the number of persons who have shaken hands an odd number of times must be even!

It is fun to draw a graph with vertices representing people and edges representing handshakes. Trying to construct a graph with an odd number of odd vertices is a quick way to convince yourself of the correct answer.

5 Helpful 0 Interesting 0 Brilliant 0 Confused

When 2 persons shake hands, with each other only one handshake should occur right ?

Arnav Das - 5 years, 1 month ago

Log in to reply

Yes Arnav you are right. But now suppose no-one else shakes hands. If you were to take a survey of everyone at the party, asking people how may times they had shaken hands, both of these people would say that they had shaken hands once and so I count this as two handshakes. If you really don't like this you can replace my 'handshake' with the term 'half-handshake', and the argument will still work.

Peter Macgregor - 5 years, 1 month ago

I agree with Arnav. I think many people would interpret the question's wording to be asking about the number of handshakes that occurred instead of the number of people each person claimed they shook hands with.

David Ortiz - 5 years, 1 month ago

Given that way the problem was written, is it true that "If there are infinitely many attendees, we can have an odd number of people shake hands an odd number of times"?

(Note that infinity is not an integer, so it is neither odd nor even)

Calvin Lin Staff - 5 years, 1 month ago

Log in to reply

I think it is possible if there are countably infinite number of people. Here's how:

i. Let's label the people 1st, 2nd, 3rd and so on. Since the number of people are countably infinite, the labelling is synonymous to creating a bijection between the set of people and the set of natural numbers. This bijection exists by definition.

ii. Now consider the following pattern: 1st person shakes hand with the 2nd person, 2nd person shakes hand with the 3rd person, 3rd person shakes hand with the 4th person, and so on.

So the 1st person only had one handshake. But every nth person had two handshakes, one with (n-1)th person and the other one with (n+1)th person, for all n > 1. So, an odd number of people (i.e. the 1st person) had an odd number of handshakes (i.e. one handshake) in this case.

Arsalan Jumani - 5 years, 1 month ago

Log in to reply

Nicely explained Arsalan. It was to rule out such infinite chains that I specified a finite number of attendees.

Peter Macgregor - 5 years, 1 month ago

Great! That was what I was going for! Can you post this question? Given this "old chestnut", it is not immediately apparent why it's possible to have odd number of odd handshakes when we have infinitely many people.

At it's heart, it's because the total number of (half-)handshakes is 2 × ∞ 2 \times \infty , which is neither even nor odd, hence the argument breaks down.

Calvin Lin Staff - 5 years, 1 month ago
Fred Shuman
May 21, 2016

At time 0, before anyone has shaken hands, everyone's (handshake) count is 0, which is even. Thus, the number of odd counts is even, being 0.

Each time a handshake occurs, the two participants get the parity (even/odd) of their counts "flipped."

Thus, the number of odd counts only ever changes by +2, -2, or 0 with each handshake.

And since it starts out even, it will forever be even.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

A nicely streamlined solution (+1)

Peter Macgregor - 5 years ago

If there are n people, each shakes hand (n-1) times. At total, there are n*(n-1) hand shakes. Which is even no matter n is even or odd. Am I wrong?

0 Helpful 0 Interesting 0 Brilliant 0 Confused

There's no requirement here that everyone shake everyone else's hand, which would be the maximum "interaction."

It is allowed for no handshakes to occur, or any number up from there. Any or all attendees could even shake the same other person's hand, multiple times.

Fred Shuman - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...