The Hanging Angle
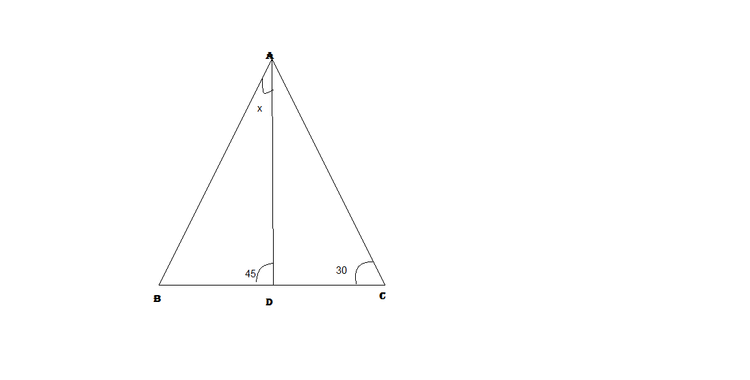 Given that
B
D
=
D
C
, find the measure of
∠
B
A
D
in degrees.
Given that
B
D
=
D
C
, find the measure of
∠
B
A
D
in degrees.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did the same way.
We draw B E ⊥ A C ( E ∈ A C ) .
Because ∠ A D B = ∠ D A C + ∠ D C A , we then have ∠ D A C = 1 5 o
Because B E ⊥ A C and ∠ A C B = 3 0 o , we then have ∠ E B D = 6 0 o and B E = 2 B C = B D , therefore we have:
- ∠ E D A = 1 5 o because ∠ E D B = 6 0 o and ∠ A D B = 4 5 o
- E D = B D
Triangle A E D has ∠ D A E = ∠ E D A = 1 5 o then E A = E D therefore E A = E B so ∠ B A E must be 4 5 o . Finally, we have ∠ B A D = 3 0 o because ∠ B A D + ∠ D A E = 4 5 o
i use the protactor 4 trolling
I solved by sine rule; later I will edit this post and write the full solution. (Need to sleep now).
Applying sine rule in both triangles ABD and ADC, I got:
sin 4 5 sin x = 2 sin 3 0 sin ( x + 4 5 )
Then, it´s not hard to get:
cos 1 5 + sin 1 5 ⋅ cot x = 2
and doing a bit more math, we get
cot x = 3 .
So, ∠ B A D = 3 0 °