A geometry problem by SKYE RZYM
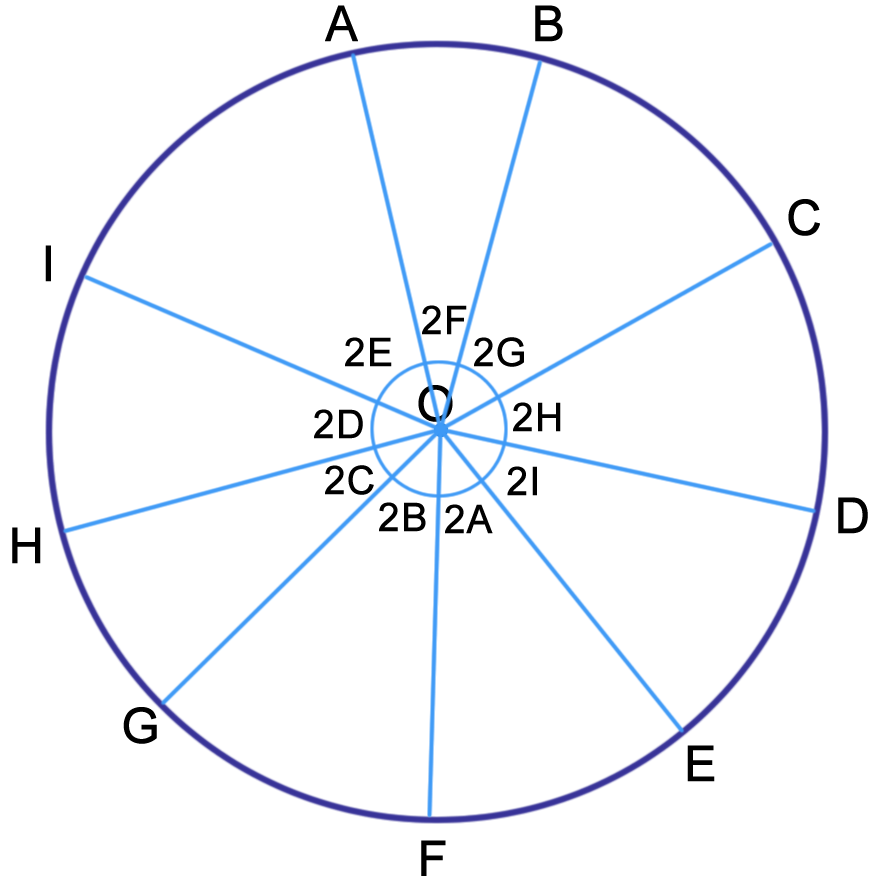
If points A , B , C , D , E , F , G , H , I all lie on a circle, as shown above, find ∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F + ∠ G + ∠ H + ∠ I in degrees.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Very neat!
Yes, Nice! Or you can reduce this complex figure to a triangle whose vertices lie on the circumference. : )
Log in to reply
How do you mean?:)
Log in to reply
Yup. Visual inspection, for us the mathematically ignorant!
Nice approach! We can use this method to find the sum of any polygon that can be inscribed in a circle.
Even if the vertices of the 9-pointed star did not lie on a circle, the sum of the angles would still remain 1 8 0 ∘ . Can we extend this solution to show that the sum of angles of any 9-pointed star of this form is 1 8 0 ∘ ?
How can the O be 2a?
Log in to reply
Circle theorem:)
Log in to reply
You call it circle theorem, I just wanna ask if there were any names else to named this theorem
An inscribed angle has a measure = 1/2 of its arc. Since all of the angles have a total arc of 360 then the sum of the angles is 180.
Ordinary 9-sided polygon would have sum of internal angles ( n − 2 ) × 1 8 0 ∘ . Self-intersecting polygon has that minus the number of times the line goes around the center times 3 6 0 ∘ . In this case
( 9 − 2 ) × 1 8 0 ∘ − 3 × 3 6 0 ∘ = 7 × 1 8 0 ∘ − 6 × 1 8 0 ∘ = 1 8 0 ∘
Nice, this method doesn't require the condition of "being inscribed in a circle". For any nine-pointed star of this form, the sum of internal angles at the vertices would be 1 8 0 ∘ .
Could you clarify what you mean by "the number of time the line goes around the center"? What line?
A classic solution worth mentioning: Take a pencil and place it on line HD. Rotate about H to HC, rotate about C to CG, and so on. The pencil traverses the star, and upon returning to HD, it has rotated 180 degrees. Since every time it rotated, it added the angle of rotation to the net rotation, the sum of the angles must be 180 degrees.
As you trace out the pattern without lifting your pencil, at every point the slope of your line increases by the included angle of the star points. Thus the slope of the penultimate line relative to the first line drawn is just the sum of all of the preceding included angles. When you arrive at the penultimate point, join it to the start position thus leaving two angles undefined, one at the start point and one at the end point. The sum of the included angles of a triangle including these two undefined angles and the last sloping line must equal 180 degrees. But this is just the sum of all of the included angles of the points. This proof does not depend on the number of points nor does it require the points to lie on a circle. QED.
Be careful, there are some kinds of stars where the sum of angles may not be 180 degrees, like this one:

We would need to modify the approach slightly to find the sum of angles in this case.
At point A (for instance), we turn over an angle of 1 8 0 ∘ − ∠ A . The total angle over which we turn when tracing the path is 1 8 0 n − ∑ ∠ i , where n = 9 is the number of angles and ∠ i runs through each of them.
Since we end up where we started, this total angle must be a multiple of 3 6 0 ∘ . If m is the number of full revolutions, then 3 6 0 m = 1 8 0 n − ∑ ∠ i or ∑ ∠ i = 1 8 0 n − 3 6 0 m .
Tracing the path carefully shows that m = 4 . But for this multiple choice question we even don't need this. After all, 1 8 0 n − 3 6 0 m = 1 8 0 ( n − 2 m ) is a multiple of 180 degrees, and there is only one option given for which this is true.
The answer is 1 8 0 ( 9 − 2 ⋅ 4 ) = 1 8 0 ⋅ 1 = 1 8 0 ∘ .
There are 9 points. Only 2 of the solutions were divisible by 9 with a whole number, 90 and 180. Eyeballed it and saw the surface area of the shaded part was more than a quarter of the circle which leaves 180
Why must the answer be divisible by 9?
It's a 9 sided polygon that crosses itself 4 times. So ( 9 − 2 ⋅ 4 ) ( 1 8 0 ) = ( 9 − 8 ) ⋅ 1 8 0 = 1 8 0
This is a modified formula of the sum of the interior angles of and exterior polygon being ( n − 2 ) ⋅ 1 8 0 ⟺ 1 8 0 n − 3 6 0
Since it crosses itself 3 times, and the fourth closes itself, then we multiply 360 with 4. Generally 1 8 0 n − 3 6 0 c ⟺ 1 8 0 ( n − 2 c ) with n sides and c crosses/closures.
Never seen that interesting formula before, but what do you mean by "crosses itself"? If I find the intersections of edges I get way more than 4.
B F can be seen as a rotation of A F F ∘ C W . Similarly, B G can be seen as a rotation of B F B ∘ C W . Continuing this pattern eventually gets you back to A F after 9 rotations. Therefore since A F is a rotation of itself at 1 8 0 ∘ C W , and this rotation was the sum of the rotations of F ∘ C W , B ∘ C W , ... E ∘ C W , and A ∘ C W .
∴ ∠ A + ∠ B + … + ∠ H + ∠ I = 1 8 0 ∘
Total circle is 2×pi. Therefore total angles makes half of it; pi.
A method from my school days for seeing that the angles in a triangle add up to 1 8 0 ∘ is to lay a pencil along one of the sides and rotate it about each of the vertices in turn. In the course of the operation, the pencil rotates through 1 8 0 ∘ in total. I essentially applied the same process to this star.
It is tempting to call the solution 180° but it isn't. I went to the trouble to actually draw it up a number of times and came sometimes close to 180° but with large deviations. I suspect there is a condition missing to make it 180°
What large deviations? Are you sure your measurements are accurate?
Using my "extreme-case" method, the maximum angle at 'A' is 180°, i.e. it would form a triangle approaching a straight line, which would cover the whole circle. (And of course, all other points, independetly of their number, here 9, would just overlap.)
Log in to reply
Yup, taking the limiting cases can give a good idea of what the answer is. We can do it because there is no restriction on the placement of the points on the circle. In this case, as we bring all the points to one point, we need to be careful while figuring out which angles tend to zero and which ones tend to 1 8 0 ∘ .
This is another type of 9-pointed star. How would we find the limiting case of this star?

If O is the centre of the circle: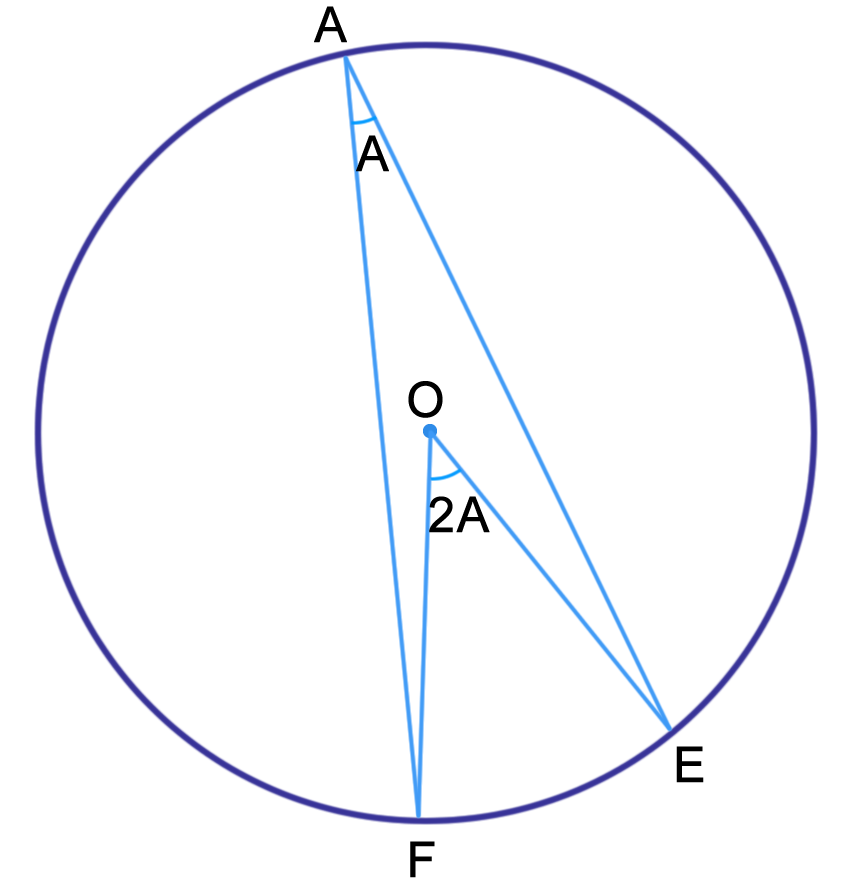 We can apply this to the entire circle:
We can apply this to the entire circle:
 Then clearly
2
∠
A
+
2
∠
B
+
2
∠
C
+
2
∠
D
+
2
∠
E
+
2
∠
F
+
2
∠
G
+
2
∠
H
+
2
∠
I
=
3
6
0
∘
.
Then clearly
2
∠
A
+
2
∠
B
+
2
∠
C
+
2
∠
D
+
2
∠
E
+
2
∠
F
+
2
∠
G
+
2
∠
H
+
2
∠
I
=
3
6
0
∘
.
So ∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F + ∠ G + ∠ H + ∠ I = 1 8 0 ∘ .