Area of a Region
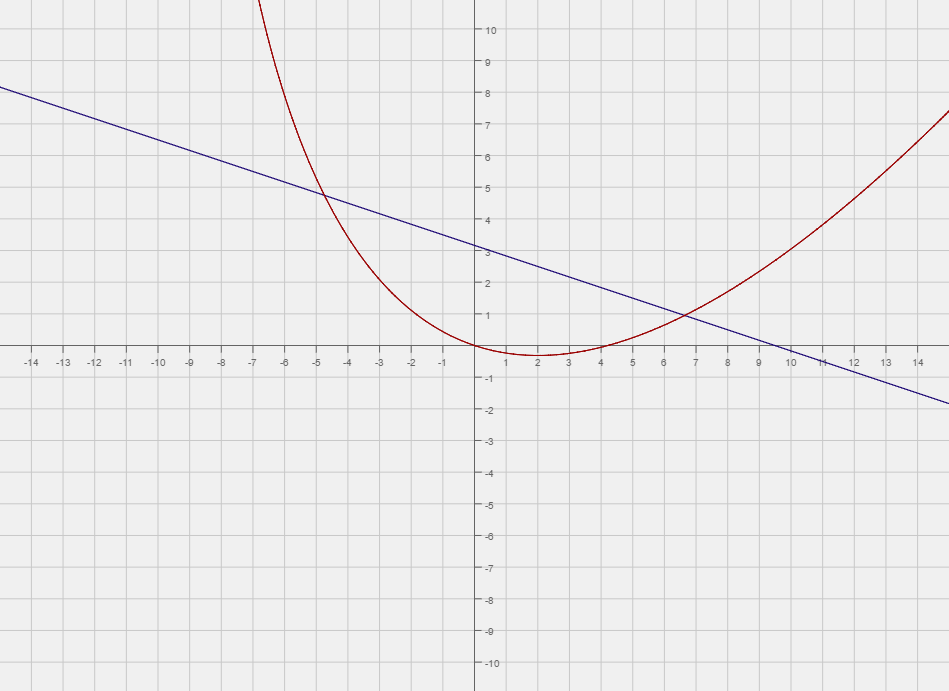
Find the region bounded by the curve and the line
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the equations of rotation to rotate the x and y axis we have:
x = x ′ c o s θ − y ′ s i n θ
y = x ′ s i n θ + y ′ c o s θ
Replacing the equations of rotation in the original equation and simplifying we obtain:
( 9 c o s 2 θ − 6 c o s θ s i n θ + s i n 2 θ ) x ′ 2 + − 2 ( 4 s i n ( 2 θ ) + 3 c o s ( 2 θ ) ) x ′ y ′ +
( 9 s i n 2 θ + 6 c o s θ s i n θ + c o s 2 θ ) y ′ 2 − 1 2 1 0 ( c o s θ + 3 s i n θ ) x ′ + 1 2 1 0 ( s i n θ − 3 c o s θ ) y ′ = 0 .
To eliminate the x ′ y ′ term set 4 s i n ( 2 θ ) + 3 c o s ( 2 θ ) = 0 ⟹ t a n ( 2 θ ) = − 4 3
⟹ t a n 2 θ = 1 − t a n 2 θ 2 t a n θ = − 4 3 ⟹
3 t a n 2 θ − 8 t a n θ − 3 = 0 ⟹ t a n θ = 6 8 ± 1 0
Choosing the positive value of t a n θ ⟹ t a n θ = 3 ⟹ c o s θ = 1 0 1 and s i n θ = 1 0 3 ⟹
x = 1 0 1 x ′ − 1 0 3 y ′
y = 1 0 3 x ′ + 1 0 1 y ′
Replacing the equations of rotation in the original equation and simplifying we obtain:
1 0 9 ( x ′ 2 − 6 x ′ y ′ + 9 y ′ 2 ) − 1 0 6 ( 3 x ′ 2 − 8 x ′ y ′ − 3 y ′ 2 ) + 1 0 1 ( 9 y ′ 2 + 6 x ′ y ′ + y ′ 2 )
− 1 2 ( x ′ − 3 y ′ ) − 3 6 ( 3 x ′ + y ′ ) = 0
⟹ y ′ 2 = 1 2 x ′
So we have a parabola in the x'y' system with focus ( 3 , 0 ) and directrix x ′ = − 3 .
− 1 0 x − 3 1 0 y + 3 0 = 0 ⟹ y = − 3 1 x + 1 0
Two point on this line are ( 0 , 1 0 ) and ( 3 1 0 , 0 )
Rotating the point ( 0 , 1 0 ) we have:
0 = 1 0 1 x ′ − 1 0 3 y ′
1 0 = 1 0 3 x ′ + 1 0 1 y ′ ⟹ ( x ′ = 3 , y ′ = 1 )
Similarily, rotating the point ( 3 1 0 , 0 ) ⟹ ( x ′ = 3 , y ′ = − 9 )
∴ In the x ′ y ′ system we have the line x ′ = 3 , and the curve y ′ 2 = 1 2 x ′ and the line x ′ = 3 intersect at ( 3 , 6 ) and ( 3 , − 6 ) ⟹
The area A = ∫ − 6 6 3 − 1 2 y ′ 2 d y ′ = 3 y ′ − 3 6 y ′ 3 ∣ − 6 6 = 2 4 .