Line Relection
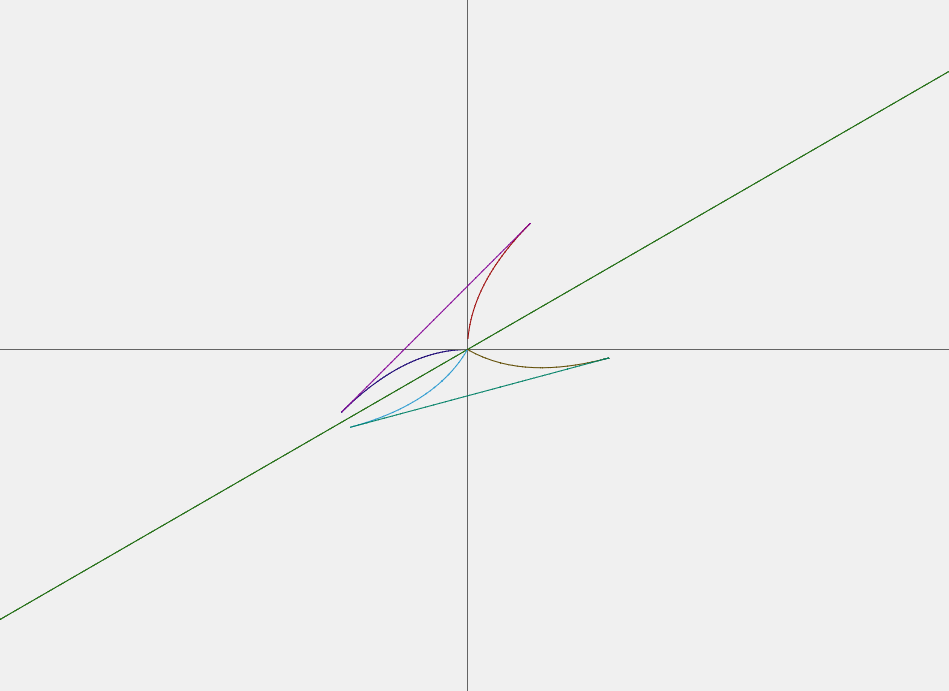
Let line L be the tangent line to the curves f ( x ) = − x 2 and g ( x ) = x .
If f ( x ) = − x 2 , g ( x ) = x and line L are reflected about the line y = 3 1 x , then the image of f ( x ) = − x 2 , g ( x ) = x and line L can be expressed as x 2 + a b x y + b y 2 + a b x − a y = 0 , b x 2 − a b x y + y 2 − a x − a b y = 0 , and a ( 1 − b ) x + a ( 1 + b ) y + 1 = 0 respectively, where a and b are coprime positive integers.
Find: a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
A vector method is perhaps an even simpler way to obtain the reflection. If e is a unit vector along the line (passing through the origin), then the image of x in the line is 2 ( x ⋅ e ) e − x . Now e = 2 1 ( 3 , 1 ) .
I am deriving the equations for a reflection abount a line L, in the event someone is not familiar with them.
Let ( x 0 , y 0 ) be a point on the line of reflection L : y − y 0 = m ( x − x 0 ) , where m = t a n θ .
Let P ( a , b ) be the point to be reflected and P ′ ( a ′ , b ′ ) be the image of P ( a , b ) ⟹
Line L is the perpendicular bisector P P ′ .
Let M : ( 2 a + a ′ , 2 b + b ′ ) be midpoint of P P ′ .
y − y 0 = m ( x − x 0 ) ⟹ y − m x = y 0 − m x 0
Line L is perpendicular to P P ′ ⟹ m P P ′ = − m 1 ⟹ m y + x = m b + a
Solving the system of equations:
m y + x = m b + a
y − m x = y 0 − m x 0
⟹ y = m 2 + 1 b m 2 + ( a − x 0 ) m + y 0 = 2 b + b ′
x = m 2 + 1 x 0 m 2 + ( b − y 0 ) m + a = 2 a + a ′
⟹ b ′ = m 2 + 1 b m 2 + 2 ( a − x 0 ) m + 2 y 0 − b
a ′ = m 2 + 1 ( 2 x 0 − a ) m 2 + 2 ( b − y 0 ) m + a
m = t a n θ = c o s θ s i n θ
Simplifying we obtain:
b ′ = ( a − x 0 ) s i n ( 2 θ ) − ( b − y 0 ) c o s ( 2 θ ) + y 0
a ′ = ( a − x 0 ) c o s ( 2 θ ) + ( b − y 0 ) s i n ( 2 θ ) + x 0
Replacing a , b , a ′ , b ′ by x , y , x ′ , y ′ we obtain:
x ′ = ( x − x 0 ) c o s ( 2 θ ) + ( b − y 0 ) s i n ( 2 θ ) + x 0
y ′ = ( x − x 0 ) s i n ( 2 θ ) − ( y − y 0 ) c o s ( 2 θ ) + y 0
f ( x ) = − x 2 and g ( x ) = x ⟹
d x d ( f ( x ) ) ∣ x = a = − 2 a and d x d ( g ( x ) ) ∣ x = b = 2 b 1 ⟹
− 2 a = 2 b 1 ⟹ a = − 4 b 1
A : ( a , − a 2 ) = ( − 4 b 1 , − 1 6 b 1 ) B : ( b , b ) ⟹
slope m ∗ = 2 b 1 = 4 b 1 ( 4 b 2 3 + 1 1 6 b 2 3 + 1 ) ⟹
1 6 b 2 3 + 1 = 8 b 2 3 + 2 ⟹ 8 b 2 3 = 1 ⟹ b = 4 1
⟹ slope m ∗ = 1 and a = − 2 1
Using A : ( − 2 1 , − 4 1 ) ⟹ y + 4 1 = x + 2 1 ⟹
4 x − 4 y + 1 = 0
4 x − 4 y + 1 = 0 is tangent to g ( x ) at B : ( 4 1 , 2 1 ) and f ( x ) at A : ( − 2 1 , − 4 1 )
For m = t a n θ = 3 1 ⟹ θ = 6 π ⟹
x ′ = 2 1 ∗ ( x + 3 y )
y ′ = 2 1 ∗ ( 3 x − y )
Using the reflection equations above: R ( y = 3 1 x )
For 4 x ′ − 4 y ′ + 1 = 0 ⟹ 2 ( 1 − 3 ) x + 2 ( 1 + 3 ) y + 1 = 0 and slope m ′ = 3 + 1 3 − 1 .
For y ′ = − x ′ 2 ⟹ x 2 + 2 3 x y + 3 y 2 + 2 3 x − 2 y = 0
and line 4 x ′ − 4 y ′ + 1 = 0 is tangent to x 2 + 2 3 x y + 3 y 2 + 2 3 x − 2 y = 0 at
( − 4 1 − 8 3 , − 4 3 + 8 1 )
For y ′ = x ′ ⟹ 3 x 2 − 2 3 x y + y 2 − 2 x − 2 3 y = 0
and line 4 x ′ − 4 y ′ + 1 = 0 is tangent to 3 x 2 − 2 3 x y + y 2 − 2 x − 2 3 y = 0 at
( 8 1 + 4 3 , 8 3 − 4 1 )
∴ a = 2 , b = 3 ⟹ a + b = 5 .
Note: I provided additional information that's not needed for the solution of the problem, but it was helpful in sketching the graph above.