Moment of Inertia
The moment of inertia of a lamina S : x 2 + y 2 = 1 , ( 0 ≤ z ≤ h ) of unit density about the line z = 2 h in the x z p l a n e can be represented by π ⋅ h ( a h 2 + b ) , where g cd ( a , b ) = 1 .
Find: a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
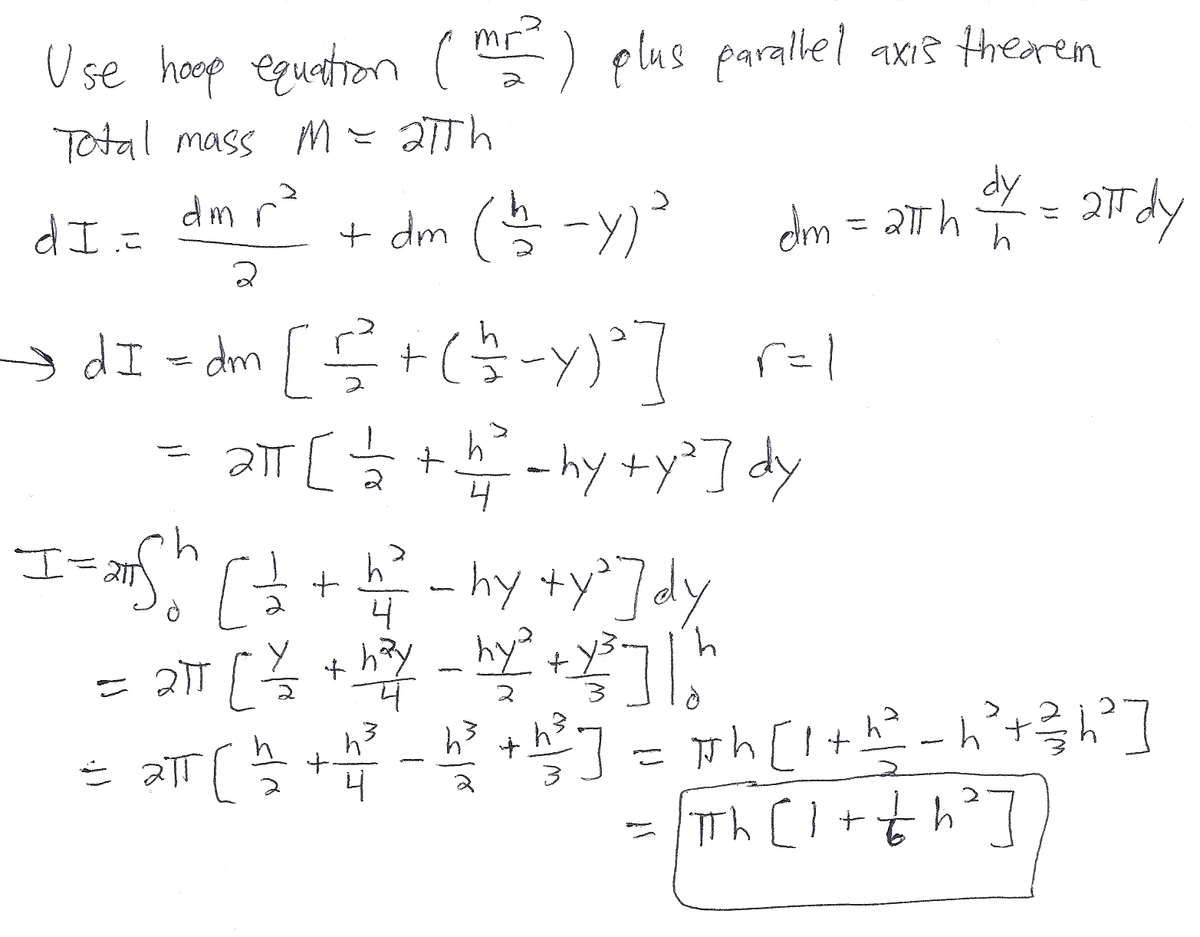
I was amazed when I first learnt about the Parallel Axis Theorem , and how it could greatly simplifies calculating moment of inertia through an arbitrary axis.
Log in to reply
Yeah, it's great. My general approach is either to use the PAT or represent it as a double (or triple) integral and compute it numerically.
Two points on line z = 2 h in the x z p l a n e are:
A : ( 0 , 0 , 2 h ) a n d B : ( 1 , 0 , 2 h ) ⟹
Line A B i s : x = t , y = 0 , z = 2 h , where the direction numbers of line A B a r e u = i + 0 j + 0 k
Let P : ( x , y , z ) be a point not on line A B and v = x i + y j + ( z − 2 h ) k be vector from point A t o P .
The distance d from point P to line A B is: d = ∣ u ∣ ∣ u X v ∣
u X v = 0 i + − ( z − 2 h ) j + y k a n d ∣ u ∣ 2 = 1 ⟹
d 2 = ( z − 2 h ) 2 + y 2
for x 2 + y 2 = 1 , ( 0 < = z < = h ) ⟹ r ( u , z ) = c o s ( u ) i + s i n ( u ) j + z k where ( 0 < = u < = 2 π ) and ( 0 < = z < = h ) ⟹
r u = − s i n ( u ) i + c o s ( u ) j + 0 k , and r z = 0 i + 0 j + k ⟹
r u X r z = c o s ( u ) i + s i n ( u ) j + 0 k ⟹ ∣ r u X r z ∣ = 1
⟹ d A = ∣ r u X r z ∣ d u d z = d u d z
and, d 2 = ( z − 2 h ) 2 + y 2 = z 2 − h z + 4 h 2 + s i n 2 ( u ) ⟹
∫ ∫ S d 2 d A = ∫ 0 h ∫ 0 2 π ( z 2 − h z + 4 h 2 + s i n 2 ( u ) ) d u d z =
∫ 0 h ( ( z 2 − h z + 4 h 2 ) ∗ u + 2 1 ∗ ( u − 2 1 s i n ( 2 u ) ) ) ∣ 0 2 π d z =
2 π ∗ ∫ 0 h z 2 − h z + 4 h 2 + 2 1 d z = 2 π ∗ ( 3 z 3 − 2 h ∗ z 2 + 4 h 2 ∗ z + 2 z ) ∣ 0 h = 2 π ( 1 2 h 3 + 2 h )
= 6 π ∗ h ∗ ( h 2 + 6 ) = π ∗ h ( 6 h 2 + 1 ) = π ∗ h ( a h 2 + b ) ⟹ a + b = 7 .