Area of a Region
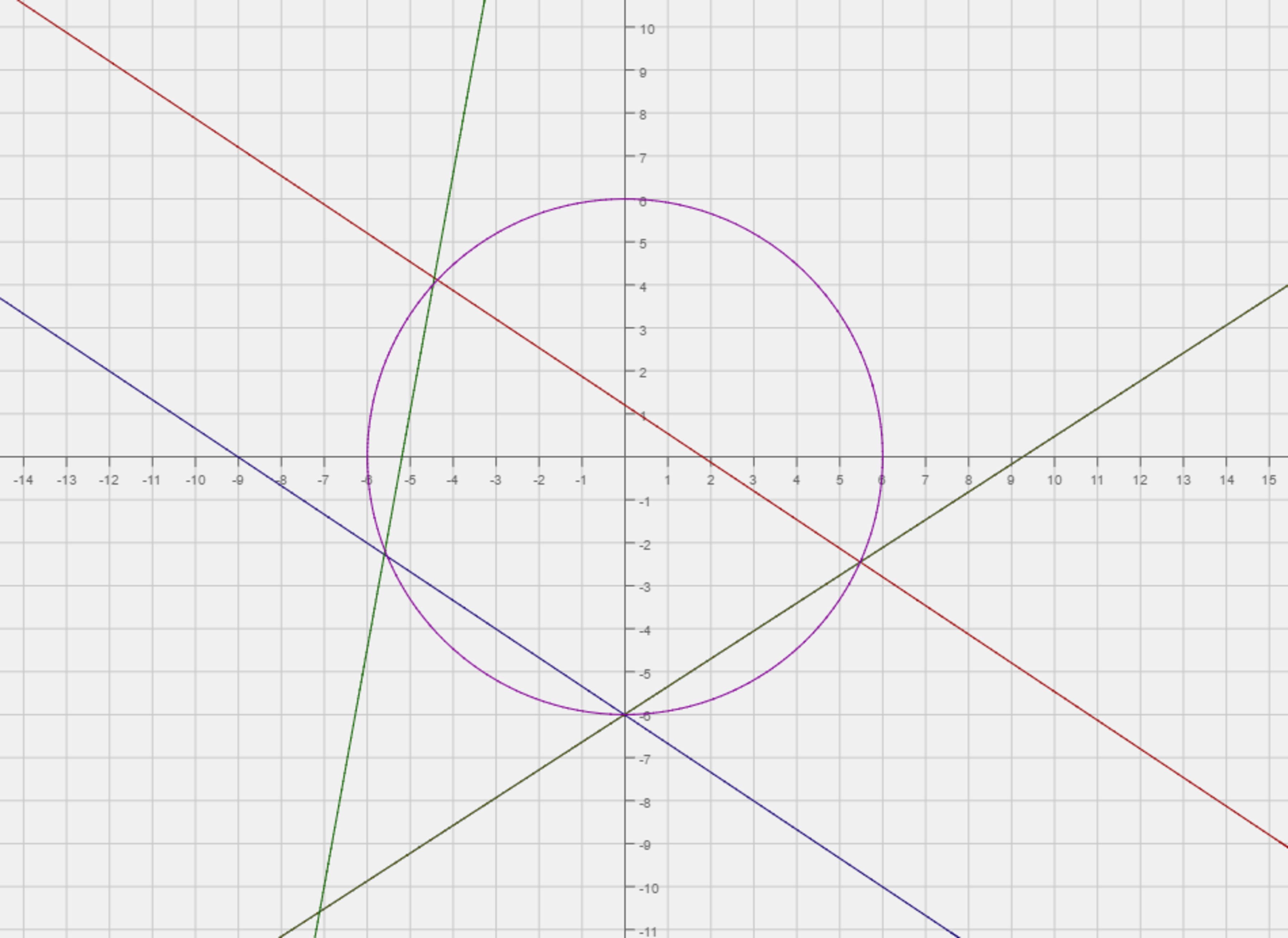
The graph of 4 x 2 + 1 2 x y + 9 y 2 + 8 1 3 x + 1 2 1 3 y − 6 5 = 0 are two parallel lines.
If 4 x 2 + 1 2 x y + 9 y 2 + 8 1 3 x + 1 2 1 3 y − 6 5 = 0 and the circle x 2 + y 2 = 3 6 intersect at four points and the area of the enclosed trapezoid formed inside the circle can be represented by a ∗ ( b + c ) , where a , b , , a n d c are coprime positive integers.
Find: a + b + c .
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the problem, can you clarify that "enclosed trapezoid formed inside the circle" refers to the area of this trapezoid?
I think the solution would have been a lot clearer if you directly factorized the equation into the 2 parallel lines, and proceeded to solve for the intersection points. It is not clear to me what value is added by converting to x ′ y ′ system.
Log in to reply
The reason being is the following:
It was very easy to work in the x'y' system, and since I had already done a similar problem with the exact same equation, I just copied the conversion to the x'y' system from my previous solution.
I failed to realize that I didn't mention the area of the trapezoid. I added it.
Are you capable of editing the problem? If so, since it was just a matter of three words, you could edit it.
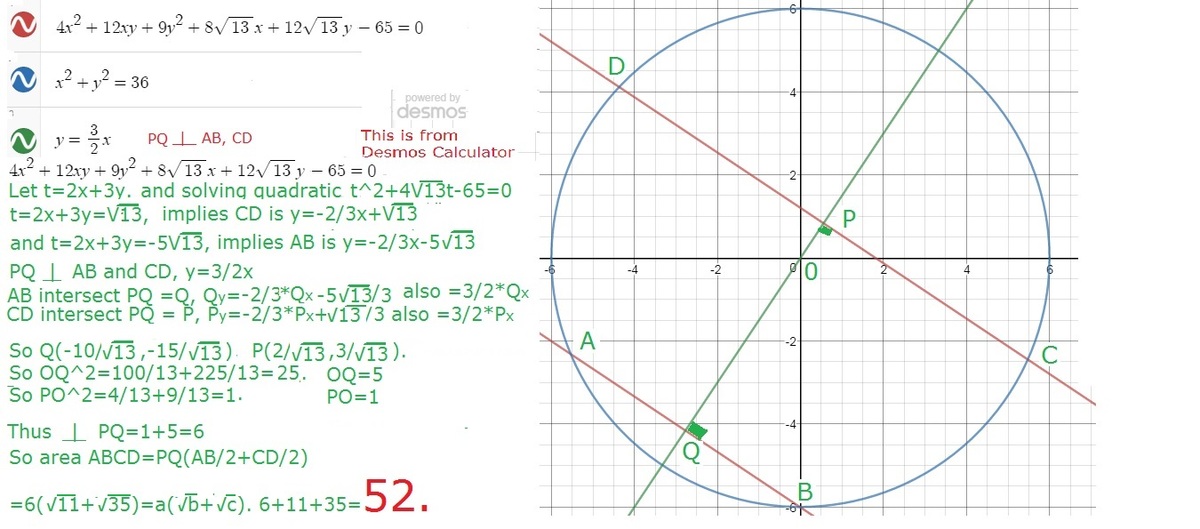
Using the equations of rotation to rotate the x and y axis we have:
x = x ′ c o s θ − y ′ s i n θ
y = x ′ s i n θ + y ′ c o s θ
Replacing the equations of rotation in the original equation and simplifying we obtain:
( 4 c o s 2 θ + 1 2 c o s θ s i n θ + 9 s i n 2 θ ) x ′ 2 + ( 4 s i n 2 θ − 1 2 c o s θ s i n θ + 9 c o s 2 θ ) y ′ 2 +
( 1 2 1 3 s i n θ + 8 1 3 c o s θ ) x ′ + ( 1 2 1 3 c o s θ − 8 1 3 s i n θ ) y ′ + ( 5 s i n ( 2 θ ) + 1 2 c o s ( 2 θ ) ) x ′ y ′ − 6 5 = 0
To eliminate the x ′ y ′ term let 5 s i n ( 2 θ ) + 1 2 c o s ( 2 θ ) = 0 ⟹
t a n ( 2 θ ) = 5 − 1 2 ⟹ 1 − t a n 2 θ 2 t a n θ = 5 − 1 2 ⟹
6 t a n 2 θ − 5 t a n θ − 6 = 0 ⟹ t a n θ = 1 2 5 + − 1 3
Choosing the positive value for t a n θ ⟹ t a n θ = 2 3 ⟹ c o s θ = 1 3 2 a n d s i n θ = 1 3 3 ⟹
x = 1 3 2 x ′ − 1 3 3 y ′ a n d y = 1 3 3 x ′ + 1 3 2 y ′
Replacing the equations of rotation in the original equation and simplifying we obtain:
1 6 9 x ′ 2 + 6 7 6 x ′ − 8 4 5 = 0 ⟹ x ′ 2 + 4 x ′ − 5 = 0 ⟹ ( x ′ + 5 ) ( x ′ − 1 ) = 0
∴ we have two parallel lines x ′ = 1 a n d x ′ = − 5 in the x ′ y ′ system.
Since the circle x 2 + y 2 = 3 6 is invariant under any rotation, we can write:
x ′ 2 + y ′ 2 = 3 6
For x ′ = − 5 ⟹ y ′ = + − 1 1 and x ′ = 1 ⟹ y ′ = + − 3 5
∴ The points of intersection of the circle and the parallel lines in the x'y' system are:
A : ( − 5 , − 1 1 ) , B : ( − 5 , 1 1 ) , C : ( 1 , 3 5 ) , , a n d D : ( 1 , − 3 5 )
so that, A B = 2 ∗ 1 1 , C D = 2 ∗ 3 5 and the height h = 6 ⟹
Area of trapezoid A B C D = 1 / 2 ∗ ( 6 ) ∗ ( 2 ∗ 3 5 + 2 ∗ 1 1 ) = 6 ∗ ( 3 5 + 1 1 ) = a ∗ ( b + c )
⟹ a + b + c = 5 2 .