A calculus problem by Rocco Dalto

Calculus Level 5

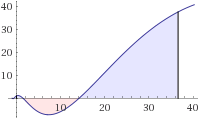
The solution to the differential $\dfrac{d^2y}{dx^2} - \dfrac{1}{x + 1} \dfrac{dy}{dx} + \dfrac{4}{(x + 1)^2} y = 0$ , with initial conditions $y(0) = 1$ , $y'(0) = 1$ can be expressed as the the curve $y = f(x)$ .

The area of the above curve $y = f(x)$ from $x = 0$ to $x = e^{\frac{2\pi}{\sqrt{3}}} - 1$ can be expressed as $\frac{m}{n} * (e^{\frac{p\pi}{\sqrt{q}}} - r )$ , where $m$ , $n$ , $p$ , $q$ , and $r$ are coprime positive integers.

Find: $m + n + p + q + r .$

Hint: Use (and/or) prove the statement below:

Let $\dfrac{d^2y}{dx^2} + P(x) \dfrac{dy}{dx} + Q(x) y = 0$ and change the independent variable from $x$ to $z = z(x)$ , where z(x) is an unspecified function of $x$ .

Show that the differential above can be transformed in this way into an equation with constant coefficients if and only if $\dfrac{Q' + 2PQ}{Q^{\frac{3}{2}}}$ is constant, in which case $z = \int \sqrt{Q(x)} \: dx$ will affect the desired result.

Note: If you which to construct such a differential choose a $P(x)$ and a real constant $j$ and solve $\dfrac{dQ}{dx} + 2 P(x) Q = j * Q^{\dfrac{3}{2}}$ for $Q(x)$ , by letting $w = Q^{-\dfrac{1}{2}}$ .

The answer is 17.

2 solutions

Rocco Dalto
Nov 27, 2016

We reduce $\dfrac{d^2y}{dx^2} - \dfrac{1}{x + 1} \dfrac{dy}{dx} + \dfrac{4}{(x + 1)^2} y = 0$ to a second order differential with constant coefficients by letting $z = 2 * \ln(x + 1)$ .

Note: From the statement above(Hint), $\dfrac{Q' + 2PQ}{Q^{\frac{3}{2}}} = -2 \implies z = \int \sqrt{Q(x)} \: dx = 2 * \int \dfrac{1}{x + 1} \: dx = 2 * ln(x + 1)$ will reduce the above differential to a second order differential with constant coefficients.

$z = 2 * \ln(x + 1) \implies$

$\dfrac{dy}{dx} = \dfrac{dy}{dz} * (\dfrac{2}{x + 1}) \implies$

and,

$\dfrac{d^2 y}{dx^2} = \dfrac{d}{dx}(\dfrac{dy}{dz} * \dfrac{2}{x + 1}) = 2 * (\dfrac{dy}{dz}(-\dfrac{1}{(x + 1)^2}) + \dfrac{1}{(x + 1)} \dfrac{d}{dx}(\dfrac{dy}{dz})) =$

$2 * (\dfrac{-1}{(x + 1)^2} \dfrac{dy}{dz} + \dfrac{1}{(x + 1)} \dfrac{d}{dz}(\dfrac{dy}{dz}) \dfrac{2}{(x + 1)}) =$

$\dfrac{4}{(x + 1)^2} \dfrac{d^2y}{dz^2} - \dfrac{2}{(x + 1)^2} \dfrac{dy}{dz}$

Replacing $\dfrac{dy}{dx}$ and $\dfrac{d^2y}{dx^2}$ into the above differential we obtain:

$\dfrac{d^2y}{dx^2} - \dfrac{dy}{dx} + y = 0 \implies m^2 - m + 1 = 0 \implies m = \dfrac{1}{2} \pm \dfrac{\sqrt{3}}{2}i \implies$

$y(z) = e^{\dfrac{z}{2}} * (c1 * cos(\dfrac{\sqrt{3}}{2} z) + c2 * sin(\dfrac{\sqrt{3}}{2} z)) \implies$

$y(x) = (x + 1) * (c1 * cos(\sqrt{3} * ln(x + 1)) + c2 * sin(\sqrt{3} * ln(x + 1)))$

and,

$\dfrac{dy}{dx} = (\sqrt{3} * c2 + c1) * cos(\sqrt{3} * ln(x + 1)) + (c2 - \sqrt{3} * c1) * sin(\sqrt{3} * ln(x + 1))$

Using the initial conditions: $y(0) = 1$ and $y'(0) = 1 \implies$ $y(x) = (x + 1) * ( cos(\sqrt{3} * ln(x + 1)))$

Let $I(x) = \int (x + 1) * ( cos(\sqrt{3} * ln(x + 1))) \: dx$

Let $u = cos(\sqrt{3} * ln(x + 1)), dv = (x + 1) \: dx \implies$ $du = -\dfrac{\sqrt{3}}{x + 1} * sin(\sqrt{3} * ln(x + 1)) \: dx$ and $v = \dfrac{(x + 1)^2}{2} \implies$

$I(x) = \dfrac{(x + 1)^2}{2} * cos(\sqrt{3} * ln(x + 1)) + \dfrac{\sqrt{3}}{2} * \int (x + 1) * sin(\sqrt{3} * ln(x + 1)) \: dx$

Let $u = sin(\sqrt{3} * ln(x + 1)), dv = (x + 1) \: dx \implies$ $du = \dfrac{\sqrt{3}}{x + 1} * cos(\sqrt{3} * ln(x + 1)) \: dx$ and $v = \dfrac{(x + 1)^2}{2} \implies$

$I(x) = \dfrac{(x + 1)^2}{2} * (cos(\sqrt{3} * ln(x + 1)) + \dfrac{\sqrt{3}}{2} * sin(\sqrt{3} * ln(x + 1))) - \dfrac{3}{4} * I(x) \implies$

$\dfrac{7}{4} * I(x) = \dfrac{(x + 1)^2}{2} * (cos(\sqrt{3} * ln(x + 1)) + \dfrac{\sqrt{3}}{2} * sin(\sqrt{3} * ln(x + 1))) \implies$

$I(x) = \dfrac{2}{7} * \dfrac{(x + 1)^2}{2} * (cos(\sqrt{3} * ln(x + 1)) + \dfrac{\sqrt{3}}{2} * sin(\sqrt{3} * ln(x + 1)))$

$\implies$

Area $A = I(x)|_{0}^{(e^{\frac{2\pi}{\sqrt{3}}} - 1)} =$ $\dfrac{2}{7} * (e^{\frac{4\pi}{\sqrt{3}}} - 1) = \frac{m}{n} * (e^{\frac{p\pi}{\sqrt{q}}} - r )$

$\implies m + n + p + q + r = 17.$

Oh wow. That's very instructive!

Calvin Lin Staff - 4 years, 6 months ago

Mark Hennings
Nov 30, 2016

Similarly to the previous problem of this type, we can look for solutions of the form $y = (x+1)^m$ . These will work provided that $m(m-1) - m + 4 \; = \; 0$ and hence $m = 1 \pm i\sqrt{3}$ . Matching the initial conditions gives $y = \tfrac12(x^{1+i\sqrt{3}} + x^{1-i\sqrt{3}})$ . Keeping the complex numbers in makes the integral easy, being $\tfrac12\left[ \frac{1}{2+i\sqrt{3}}x^{2+i\sqrt{3}} + \frac{1}{2-i\sqrt{3}}x^{2-i\sqrt{3}}\right]_0^{ e^{\frac{2\pi}{\sqrt{3}}} - 1 } \; = \; \tfrac27\big(e^{\frac{4\pi}{\sqrt{3}}} - 1\big)$ making the answer $\boxed{17}$ .

The last three differential equations I constructed are of the the same type. That is, they use the same theorem and construction. The last one I used was the following differential equation below.

$\dfrac{d^2y}{dx^2} - \dfrac{1}{x(x + 1)} \dfrac{dy}{dx} + \dfrac{x^2}{(x + 1)^2 (x - \ln(x + 1))^2} y = 0$

If $y_1(x)$ and $y_2(x)$ are linear independent solutions to the differential equation above.

Evaluate: $\displaystyle \int_{0}^{e - 1} y_1(x)^2 + y_2(x)^2 \, dx$ .

Express the result to 6 decimal places.

Is there a simple substitution that would work here?

Rocco Dalto - 4 years, 6 months ago

"Of this type"...

The previous problem of yours I posted a solution was a DE of the form $x^2 y'' + Axy'(x) + By(x) = 0$ with constants $A,B$ . Equations of this type always permit solutions of the form $y = x^a$ , provided that $a(a-1) + Aa + B = 0$ , a quadratic equation in $a$ , whose two roots give the two solutions. This one just goes with powers of $x+1$ instead.

My other comment in both cases is that the integration is much easier using complex numbers.

Mark Hennings - 4 years, 6 months ago

A calculus problem by Rocco Dalto

The answer is 17.

2 solutions

0 pending reports