A calculus problem by Rocco Dalto
d t d x = − y + x ( 1 − x 2 − y 2 ) d t d y = x + y ( 1 − x 2 − y 2 )
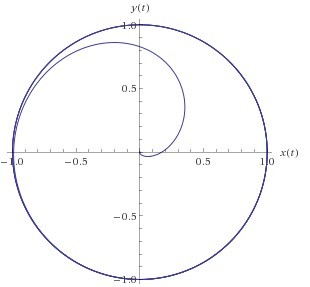
The nonlinear system above has the solution x = x ( t ) , y = y ( t ) , where x ( t = 0 ) = y ( t = 0 ) = 2 1 .
If
∫
0
ln
(
3
)
x
(
t
)
2
+
y
(
t
)
2
d
t
can be expressed as
ln
(
α
+
λ
α
+
β
)
, where
α
,
β
, and
λ
are coprime positive integers.
Find: α + β + λ .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
d t d x = − y + x ( 1 − x 2 − y 2 ) d t d y = x + y ( 1 − x 2 − y 2 )
Converting to polar coordinates, let x = r c o s θ , y = r s i n θ ( 1 ) : x 2 + y 2 = r 2 , ( 2 ) : θ = arctan ( x y )
Taking the derivatives with respect to t of ( 1 ) and ( 2 ) we obtain:
r d t d r = x d t d x + y d t d y
r 2 d t d θ = x d t d y − y d t d x
x ∗ ( d t d x = − y + x ( 1 − x 2 − y 2 ) ) y ∗ ( d t d y = x + y ( 1 − x 2 − y 2 ) )
Adding the above equations we obtain: r d t d r = r 2 ( 1 − r 2 ) ⟹ d t d r = r ( 1 − r 2 )
and, − y ∗ ( d t d x = − y + x ( 1 − x 2 − y 2 ) ) x ∗ ( d t d y = x + y ( 1 − x 2 − y 2 ) )
Adding the above equations we obtain:
r 2 d t d θ = r 2 ⟹ d t d θ = 1
The system of differentials above has a single critical point at r = 0 . Assuming r > 0 , the system above reduces to:
d t d r = r ( 1 − r 2 ) d t d θ = 1
⟹ ∫ r ( 1 − r 2 ) d r = ∫ d t ⟹
∫ r 1 + 2 ( 1 − r ) 1 − 2 ( 1 + r ) 1 d r = ∫ d t ⟹
ln ( 1 − r 2 r ) = t + K ⟹ 1 − r 2 r 2 = C e 2 t ⟹
r 2 ( 1 + C e 2 t ) = C e 2 t ⟹ r = 1 + C e 2 t C e 2 t ⟹ r = 1 + C e − 2 t 1 and, θ = t + t 0
x = r c o s ( t + t 0 ) , y = r s i n ( t + t 0 ) ⟹
x ( t ) = 1 + C e − 2 t c o s ( t + t 0 ) y ( t ) = 1 + C e − 2 t s i n ( t + t 0 )
Using initial conditions x ( t = 0 ) = y ( t = 0 ) = 2 1 we obtain:
4 1 ( 1 + C ) = c o s 2 ( t 0 )
4 1 ( 1 + C ) = s i n 2 ( t 0 )
⟹ 2 1 ( 1 + C ) = 1 ⟹ C = 1 ⟹
x ( t ) = 1 + e − 2 t c o s ( t + t 0 ) y ( t ) = 1 + e − 2 t s i n ( t + t 0 )
Note: Using C = 1 ⟹ t 0 = 4 π here, but it's not needed for the integral below.
The integral I = ∫ 0 ln ( 3 ) x ( t ) 2 + y ( t ) 2 d t =
∫ 0 ln ( 3 ) e 2 t + 1 e t d t
Let e t = t a n θ ⟹ d t = t a n θ s e c 2 ( θ ) d θ ⟹
I = ∫ 0 ln ( 3 ) e 2 t + 1 e t d t = ∫ 4 π 3 π s e c ( θ ) d θ = ln ( s e c ( θ ) + t a n ( θ ) ) ∣ 4 π 3 π =
ln ( 2 + 1 2 + 3 ) = ln ( α + λ α + β )
⟹ α + β + λ = 6