A problem by Rohit Dhiman
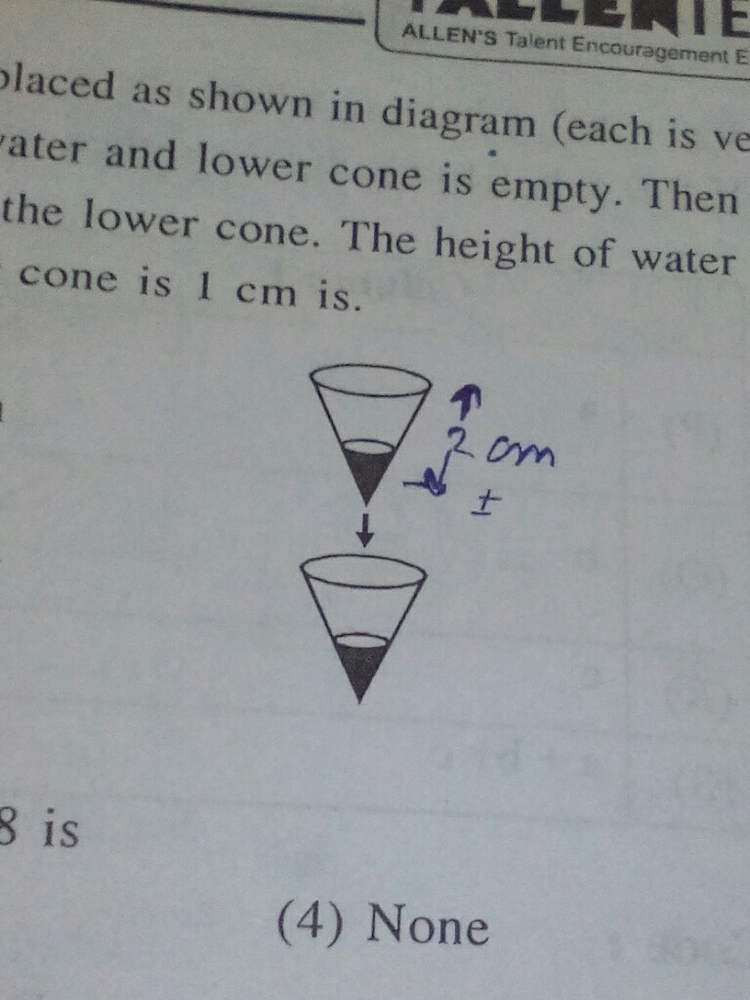 Two identical right circular cones each of height 2cm are placed as shown in diagram (each is vertical apex downward), At the start 'upper cone is full of water and lower cone is empty. Then water drips through a hole in the apex of upper cone into lower cone . The height of water in the cone at the moment when height of water in the upper cone is 1cm is.
Two identical right circular cones each of height 2cm are placed as shown in diagram (each is vertical apex downward), At the start 'upper cone is full of water and lower cone is empty. Then water drips through a hole in the apex of upper cone into lower cone . The height of water in the cone at the moment when height of water in the upper cone is 1cm is.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Sorry about the diagrams. I do not have a great drawing tool for figures.
Consider, the top cone, as shown above in the diagram. From the simple geometry of the figure, we have,
h H = r R ⟹ 1 2 = r R ⟹ r = 2 R
Initial volume of water in the top cone Final volume of water in the top cone Change in volume of water = = = = = = = = 3 1 π R 2 H 3 1 π R 2 ⋅ 2 3 2 π R 2 3 1 π r 2 h 3 1 π 4 R 2 ⋅ 1 1 2 π R 2 π R 2 ( 3 2 − 1 2 1 ) 1 2 7 π R 2
This volume of water is now filled in the next cone.
Consider the bottom cone after the water has filled some portion of it (which has height h to be calculated), as shown below in the diagram. again, we have,
h H = r R ⟹ h 2 = r R ⟹ r 2 R 2 = h 2 4
Now, volume of water filled in this cone can be represented as: 3 1 π r 2 h
∴ 3 1 π r 2 h ⟹ h ⟹ h ⟹ h ⟹ h 3 ⟹ h = = = = = = 1 2 7 π R 2 4 7 ( r 2 R 2 ) 4 7 ( h 2 4 ) h 2 7 7 3 7 cm