A geometry problem by Ronak Singha

Geometry Level pending

In the figure below points A, B, C and D are on a circle. Point O is the intersection of chords AC and BD. The area of triangle BOC is 15; the lenght of AO is 10 and the length of OB is 5. What is the area of triangle AOD?


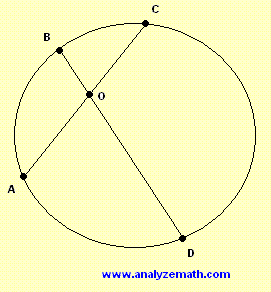
The answer is 60.

Ronak Singha by Ronak Singha , 27, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Nguyen Thanh Long
Jul 23, 2015

According to the theory for the relation between two chords that intersect in a circle that we have: O A × O C = O B × O D → O A O B = O C O D = 2 OA \times OC = OB \times OD \rightarrow \frac{OA}{OB}=\frac{OC}{OD}=2 [ A O D ] = 4 × [ B O C ] = 60 [AOD] = 4 \times [BOC] = \boxed{60}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

As △ D O A ∼ △ C O B \bigtriangleup DOA \sim \bigtriangleup COB , the proportionality constant is 2 2 , therefore the area is 15 ⋅ 2 2 = 60 15\cdot 2^2 = 60

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...