Circle problem

Recall that the form of the circle in the Cartesian plane is $(x - h)^2 + (y - k)^2 = r^2$ where

• $(h,k)$ is the center of the circle
• $r$ is the radius of the circle

Given that the circle is bounded by $x$ -axis and the graph of $y = 4$ , the center is $(h,2)$ , and the radius is $r = 2$ , which give $(x - h)^2 + (y - 2)^2 = 4$ Here is the diagram of the graphs: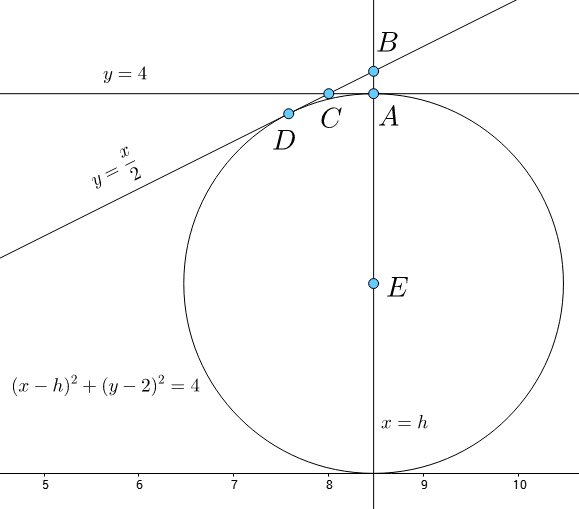 Figure 1. Graphs of lines and circle. where $A = (h,4)$ , $B = \left(h, \dfrac{h}{2}\right)$ , $C = (8,4)$ and $D$ are intersection points of the graphs. Take a careful look where I included the dashed line and shaded $\Delta BED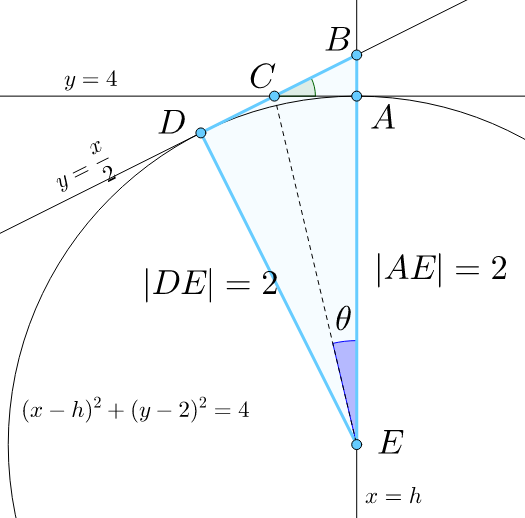$ : Figure 2. Triangular region shaded by baby blue color. From $\angle ACB$ , we work our way to determine $\theta = \angle AEC$ . The goal of this problem is to determine the measurement of $\theta = \angle AEC$ , indicated by the dark-blue color on the arc. Then, find $h$ by trigonometry.

Since the graph of $y = 4$ is parallel to $x$ -axis, the intersection of $y = \dfrac{x}{2}$ and $y = 4$ forms $\angle ACB = \arctan\left(\dfrac{1}{2}\right)$ and $\angle ACD = 180^{\circ} - \angle ACB = 180^{\circ} - \arctan\left(\dfrac{1}{2}\right)$ . Then, since $|DE| = |AE| = 2$ and both $DE \perp DC$ and $AE \perp AC$ , which implies $\angle CDE = \angle CAE = 90^{\circ}$ , this shows that $\angle AED = \arctan\left( \dfrac{1}{2}\right)$ . Thereby, $\theta = \angle AEC = \dfrac{1}{2}\arctan\left(\dfrac{1}{2}\right)$ .

So elementary trigonometry (see Note for evaluating $\arctan$ ) shows that $\begin{array}{rl} \tan\left(\theta\right) &= \dfrac{|AC|}{|AE|}\\ |AC| &= |AE|\tan\left(\theta\right)\\ &= 2\tan\left(\dfrac{1}{2}\arctan\left(\dfrac{1}{2}\right)\right)\\ &= 2\left(\sqrt{5} - 2\right)\\ &= 2\sqrt{5} - 4 \end{array}$ Thus, $\begin{array}{rl} h - 8 &= 2\sqrt{5} - 4\\ h &= \boxed{4 + 2\sqrt{5}}\\ \end{array}$

---

Note

To prove that $\tan\left(\dfrac{1}{2}\arctan\left(\dfrac{1}{2}\right)\right) = \sqrt{5} - 2$ , apply half-angle identity: $\tan\left(\dfrac{1}{2}\gamma\right) = \dfrac{1 - \cos(\gamma)}{\sin(\gamma)}$ Letting $\gamma = \arctan\left(\dfrac{1}{2}\right)$ , we have $\begin{array}{rl} \cos\left(\arctan\left(\dfrac{1}{2}\right)\right) &= \cos\left(\arccos\left(\dfrac{2}{\sqrt{5}}\right)\right)\\ &= \dfrac{2}{\sqrt{5}}\\ \sin\left(\arctan\left(\dfrac{1}{2}\right)\right) &= \sin\left(\arcsin\left(\dfrac{1}{\sqrt{5}}\right)\right)\\ &= \dfrac{1}{\sqrt{5}} \end{array}$ So $\begin{array}{rl} \tan\left(\dfrac{1}{2}\gamma\right) &= \dfrac{1 - \dfrac{2}{\sqrt{5}}}{\dfrac{1}{\sqrt{5}}} \cdot \dfrac{\sqrt{5}}{\sqrt{5}}\\ &= \sqrt{5} - 2 \end{array}$

These diagrams are done by GeoGebra .

Observe that $y=4$ and the $x - axis$ act as two parallel tangents to our circle, therefore they lie on opposite ends of a diameter of our circle. Thus, we obtain the length of diameter as $4$ units. Since the diameter is also perpendicular to the $x - axis$ , therefore the ordinate of the center of the circle will be equal to the radius of the circle which is $2$ .

Let the center of this circle be $(h,2)$ .

Since its radius is $2$ units, therefore its perpendicular distance from the third tangent, $\left( y = \dfrac x2 \equiv x - 2y = 0 \right)$ will also be $2$ units.

The distance of $(h,2)$ from the line $x - 2y = 0$ , is given by

$D = \left| \dfrac{h-4}{\sqrt5} \right| = 2$

Solving for $h$ ,

$\begin{aligned} & \left| \dfrac{h-4}{\sqrt5} \right| = 2 \\ \implies & \dfrac{{(h-4)}^2}{5} = 4 \\ \implies & h^2 - 8h - 4 = 0 \\ \implies & h = \dfrac{8 \pm \sqrt{80}}{2} \\ \implies & h = 4 \pm 2 \sqrt5 \\ \implies & h = \boxed{4 + 2 \sqrt5} \qquad \qquad \qquad \small \color{#3D99F6}{\text{As} \ \ 'h' \ \ \text{should be positive but} \ 4 - 2 \sqrt5 < 0} \end{aligned}$