Find the steady state response.

Classical Mechanics Level 3

Consider the linear time invariant system described by the transfer function,

$P(s)= \frac{1}{s^{2}+0.1s+1}$

What is the steady state response to a sinusoidal input, $u(t)=\sin(t)$ ?

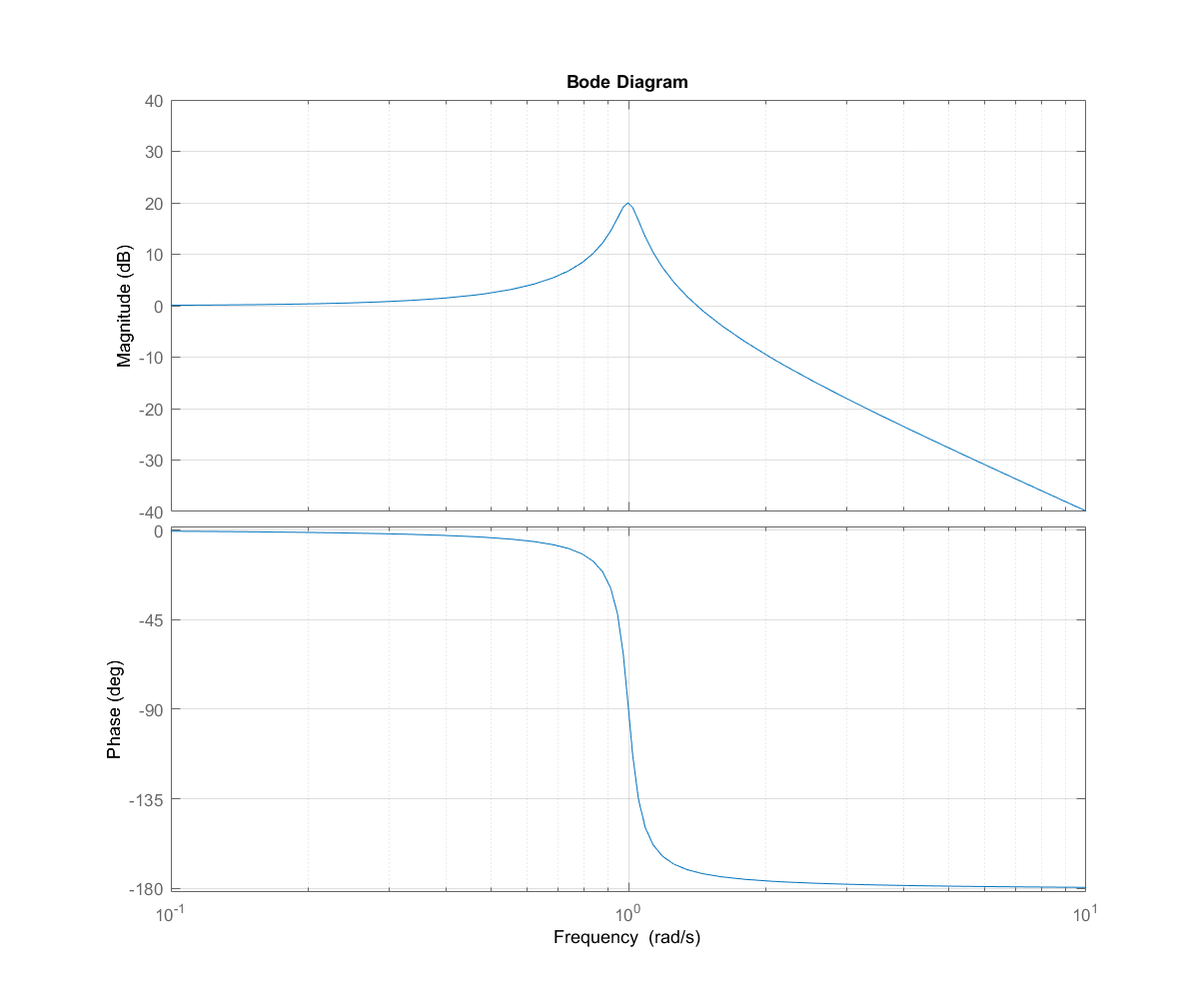
For reference a frequency response plot, called a Bode plot, is shown. Calculations can also be done numerically.

10\sin(t+\pi)

20\cos(t+\pi)

10\sin(t-\pi/2)

Asymptotically approach 1

2 solutions

Steven Chase
Apr 15, 2017

To expand on what @Samuel Hansen said in his solution, evaluate the transfer function with $s = j \omega = j$ .

$\large{P(s) = \frac{1}{s^2 + 0.1 s + 1} = \frac{1}{-1 + 0.1 j + 1} = -j10 }$

Thus, we have a gain of 10 and a phase lag of 90 degrees, corresponding to:

$\large{u'(t) = 10 sin(t - \frac{\pi}{2}})$

Samuel Hansen
Apr 12, 2017

We have a LTI system being driven by a sinusoidal input. It is one of the fundamental results of linear systems theory that the output will also be a sinusoid with the same frequency but with gain and phase determined by the gain and phase of the transfer function at that frequency.

Looking at the Bode diagram (or performing the calculations for $s=j \omega =j1$ ) we see that for 1 rad/s we have a gain of 20dB and a phase of -90 degrees. And 20 dB corresponds to a gain of 10 due to the conversion from decibels, $dB \,gain = 20log_{10} (gain)$ . Multiplying by the gain and adding the phase yields the result.

Find the steady state response.

2 solutions

0 pending reports