A geometry problem by SHANKH SURI
Geometry
Level
2
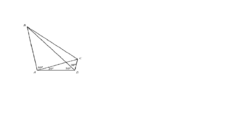 Quadrilateral ABCD has angles < BDA = < CDB = 50◦
, < DAC = 20◦
, and
< CAB = 80◦
. Find angle < DBC.
Quadrilateral ABCD has angles < BDA = < CDB = 50◦
, < DAC = 20◦
, and
< CAB = 80◦
. Find angle < DBC.
12
8.5
10
9
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
B lies on the internal bisector of ∠ A D C . The external angle to ∠ B A D is 1 8 0 ∘ − 8 0 ∘ − 2 0 ∘ = 8 0 ∘ , hence B A is the external bisector of ∠ C A D . As B also lies on the internal bisector of ∠ A D C , it follows that B is the D -excenter of △ A D C , hence B C is the external angle bisector of ∠ A D C . It's easy to find ∠ A C D = 6 0 ∘ , hence ∠ B C A = 6 0 ∘ , and ∠ D B C = 1 0 ∘ .