A geometry problem by Siba Smarak Panigrahi
Geometry
Level
4
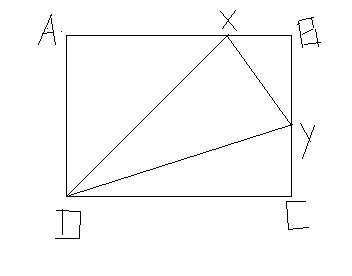ABCD is a rectangle and line DX and DY and XY are drawn where X is on AB and Y is on BC.
The area of the triangle AXD is 5, the area of triangle BXY is 4 and area of CYD is 3. Determine
the area of triangle DXY
The answer is 84.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let length (AB) & breadth (BC) respectively be l and b units.
let AX = a, then BX = l - a & let BY = c, then CY= b - c
Area of rectangle = lb . . . . . . . . . (i)
Area ∆ ADX = (1/2) AD * AX = 5 => (1/2) b * a => ab = 10 => a = 10/b . . . . . . . . (ii)
Area ∆ BXY = (1/2) BX * BY = 4 => (1/2) (l - a) *c => lc - ac = 8 => c = 8/ [l - (10/b)] = 8b/ (lb - 10) . . . . . . . (iii)
Area ∆ CYD = (1/2) DC * YC = 3 => (1/2) l * (b - c) => l[b - 8b/(lb - 10) = 6 => lb[ lb - 10 - 8] = 6(lb - 10)
now let lb = y
=> y ( y - 18) = 6 (y - 10) => y^2 - 24 y + 60 = 0
Using quadratic formula;
y = (24 ±√{(24^2 - 4 1 60)} /2 => [24 + √(576 - 240)]/2 => 12 + √(336)/2 => 12 + √(84),
therefore lb = 12 + √(84) => lb - 12 = √(84)
now, area of the ∆ XYD = [lb - 5 - 4 - 3] => lb - 12 = √x => √(84) = √x
so, x = 84