I Can See it Again! Can you?

Algebra Level 3

sin ⁡ ( e x ) = 5 x + 1 5 x \large \sin (e^x) = 5^x+ \frac 1{5^x}

How many solutions of x x satisfy the equation above?

0 3 2 Infinitely Many

Aniruddha Bagchi by Aniruddha Bagchi , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Aniruddha Bagchi
May 25, 2017

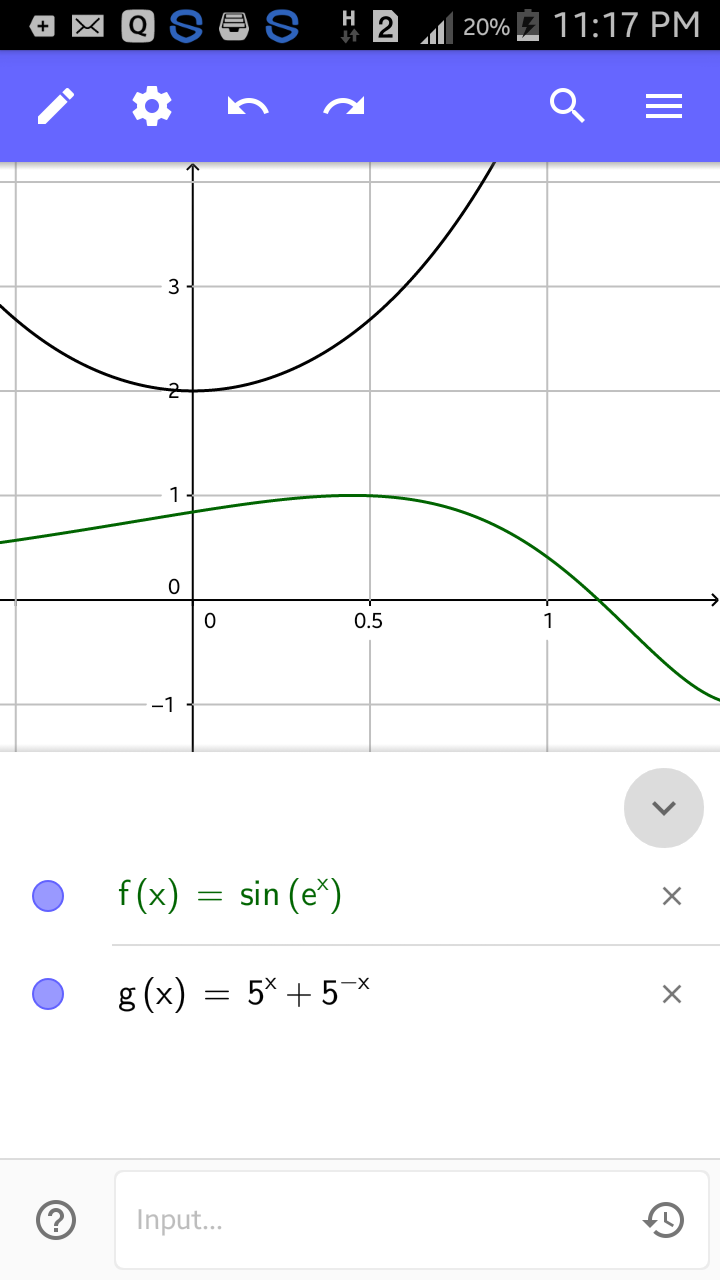
Using AM-GM Inequality, We see that 5 x 5^x +1/ 5 x 5^x can have a minimum value of 2.

But s i n ( e x ) sin(e^x) can have a maximum value of 1 because the range of any sine function lies from -1 to +1 both inclusive. So if we plot both LHS and RHS sides of the equation on graph we get no common intersections hence no solutions.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Use AM-GM inequality to RHS it will be easy

Kushal Bose - 4 years ago

Did that only ... see the first line of my solution.

Aniruddha Bagchi - 4 years ago

Log in to reply

Oh I missed out that

Kushal Bose - 4 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...