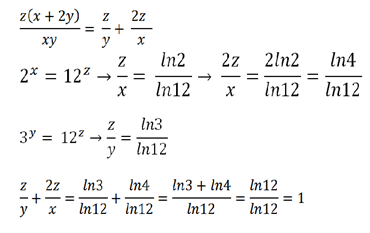1 equation 3 variables
2 x = 3 y = 1 2 z
If the equation above is fulfilled for non-zero values of x , y , z , find the value of x y z ( x + 2 y ) .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
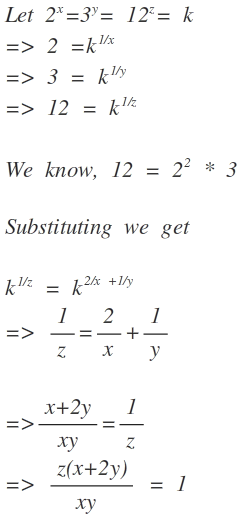
But how is this possible?
2 x and 1 2 z are always even whereas 3 y is always odd. (except for x=y=z=0)
Log in to reply
It did not say that it must be an integer, x could have a value of 1.23456789.
Log in to reply
Thank you for a wise mention. The question will be edited soon.
How value of x is calculated
I think mine looks stupid compared to other solutions but it's worth a try!
2 x = 3 y = 1 2 z
By multiplying, therefore,
2 x × 3 y = 1 2 2 z
and since 12 can be broken up into 2 2 , 3
then
2 x × 3 y = 2 4 z × 3 2 z
things getting clearer now,
therefore,
2 x = 2 4 z , 3 y = 3 2 z
then x = 4 z , y = 2 z
by substituting in the required problem,
x y z ( x + 2 y ) = 4 z × 2 z z ( 4 z + 2 ( 2 z ) ) = 8 z 2 8 z 2 = 1
I really like this solution, nice post.
Aren't you still running into the problem that you're assuming integers or at least rational numbers at the step when you split the powers of 2 off from the powers of 3?
I mean, considering the initial equation, it is easy to see that something like x = 4 z is simply not true.
You have an original mind, which is good, but I think you got lucky with this one. As Anthony Ritz already pointed out, x is not 4z. If x = 4z then
2 4 z = 1 2 z taking the log of both sides
4 z ∗ l n ( 2 ) = z ∗ l n ( 1 2 )
4 ∗ l n ( 2 ) = l n ( 1 2 ) which is not true
4 ∗ l n ( 2 ) − l n ( 1 2 ) = 0 . 2 9
very original. very good
This is the most brilliant solution.
The other way is to use lo g .
2 x = 3 y = 1 2 z ⇒ x lo g 2 = y lo g 3 = z lo g 1 2 ⇒ y = lo g 3 x lo g 2 ⇒ z = lo g 1 2 x lo g 2
x y z ( x + 2 y ) = x lo g 3 x lo g 2 lo g 1 2 x lo g 2 ( x + 2 lo g 3 x lo g 2 ) = lo g 1 2 lo g 2 ( lo g 3 lo g 3 + 2 lo g 2 ) × lo g 2 lo g 3 = lo g 1 2 × lo g 3 × lo g 2 lo g 2 × lo g 1 2 × lo g 3 = 1
I took same way. but substitute x and y in terms of z will easy these steps a bit
I took basically the same approach. BTW you have a typo: x instead of z where you quote the expression to be evaluated.
AN easy solution for this could be GIVEN that 2 x = 3 y = 1 2 z ⇒ LET 2 x = 3 y = 1 2 z = k then k x 1 = 2 , k y 1 = 3 and k z 1 = 12 "if you are careful observant you would write it as- k x 1 k x 1 k y 1 = k z 1 Further since the bases are same power could be compared and the answer would be 1
Let 2 x = 3 y = 1 2 z . This can be solved using some general term a where
x = ln 2 ln a
y = ln 3 ln a
z = ln 1 2 ln a
Such that 2 x = 3 y = 1 2 z yields
2 ln 2 ln a = 3 ln 3 ln a = 1 2 ln 1 2 ln a = a
Then substitute x , y , z in terms of a so x y z ( x + 2 y ) becomes ln 2 ln a ⋅ ln 3 ln a ln 1 2 ln a ( ln 2 ln a + 2 ln 3 ln a )
Then just simplify
ln 2 1 ⋅ ln 3 1 ln 1 2 1 ( ln 2 1 + 2 ln 3 1 )
ln 1 2 1 ⋅ ln 2 1 ⋅ ln 3 1 ln 2 ⋅ ln 3 2 ln 2 + ln 3
ln 1 2 2 ln 2 + ln 3 = ln 1 2 ln 4 + ln 3 = ln 1 2 ln 1 2 = 1
2 x = 3 y = 1 2 z = ( 2 2 × 3 ) z
2 2 = ( 2 x ) x 2 = ( 1 2 z ) x 2 = 1 2 x 2 z
3 = ( 3 y ) y 1 = ( 1 2 z ) y 1 = 1 2 y z
2 2 × 3 = 1 2 x 2 z × 1 2 y z = 1 2 x 2 z + y z = 1 2 x y z ( x + 2 y ) = ( 2 2 × 3 ) x y z ( x + 2 y )
( 2 2 × 3 ) 1 = ( 2 2 × 3 ) x y z ( x + 2 y ) ⟹ x y z ( x + 2 y ) = 1
Thanks for the solution
Let's work a bit the equation: 2 x = 1 2 z → Lower the power x times 2 x x = 1 2 x z 2 = 1 2 x z → Raise to power 2 4 = 1 2 x 2 z ( 1 ) Now let's work the second equation as well: 3 y = 1 2 z → Lower the power y times 3 y y = 1 2 y z 3 = 1 2 y z ( 2 ) Upon mutiplying the pairs of left and right sides of equations ( 1 ) and ( 2 ) we get: 4 × 3 = 1 2 x 2 z × 1 2 y z 1 2 = 1 2 x 2 z + y z 1 2 1 = 1 2 x y 2 y z + x z Since we have equal bases we can solve only for the exponents, which, as well, have to be equal: 1 = x y 2 y z + x z 1 = x y z ( x + 2 y ) That's exactly what we are asked for and so the answer is x y z ( x + 2 y ) = 1 .
Great problem Swapnil Das
I found from data x and y in terms of z and then substituted to get 1.But this is not a very elegent solution
(2^x)×(3^y)=(12^z)×(12^z) =[2^(4z)]×[3^(2z)] Comparing both side powers.... x=4z,y=2z. Put the value of x and y in given equation, z(4z+2×2z)÷(4z×2z)=1.