A geometry problem by Yahia El Haw
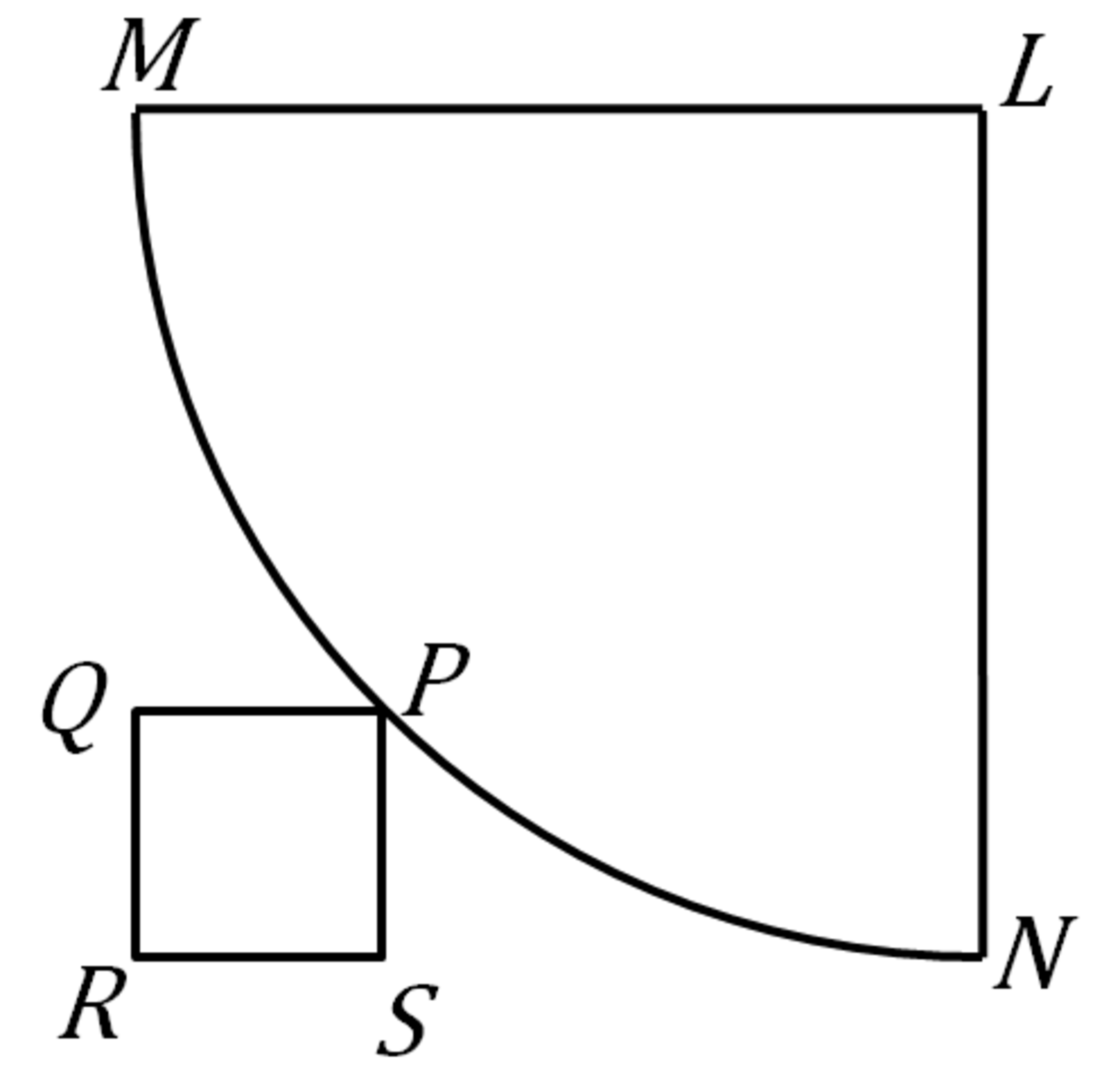
In the figure given below M L and N L are adjacent sides of a square and the arc M P N is drawn with L as centre and L M as radius. P is a point on the arc and P Q R S is a square such that, R S , if extended, passes through N while R Q , if extended, passes through M . What is the ratio of the area of a square of side M L and the square P Q R S ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Please check your letters. Do you mean N in place of L in the first line ? Similar afterwards..
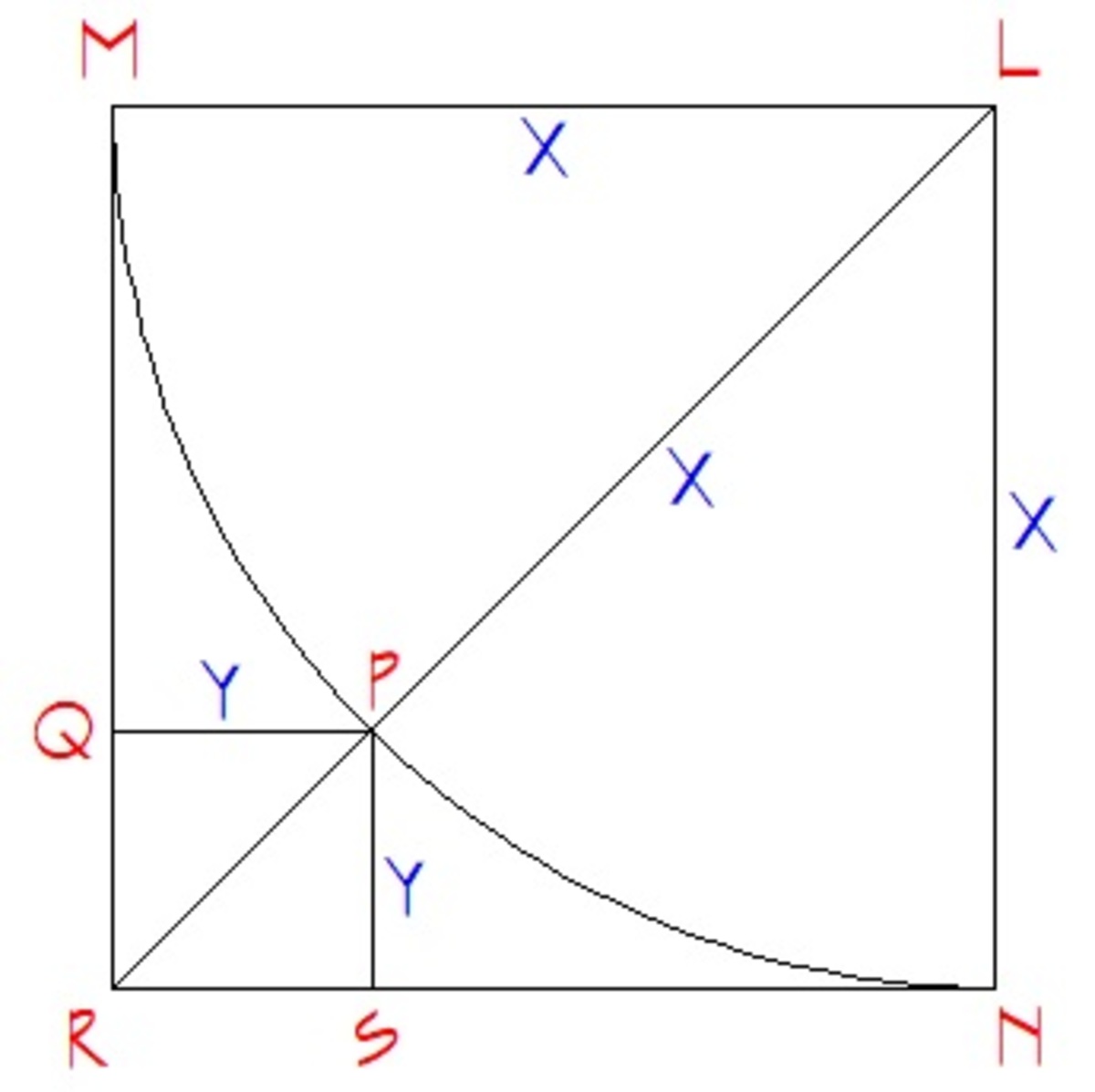 Let the side length of square
M
L
N
R
be
X
and the side length of square
Q
P
S
R
be
Y
, then
R
L
=
X
2
and
R
P
=
Y
2
.
Let the side length of square
M
L
N
R
be
X
and the side length of square
Q
P
S
R
be
Y
, then
R
L
=
X
2
and
R
P
=
Y
2
.
R L = R P + X ⟹ X 2 = Y 2 + X ⟹ Y 2 = X 2 − X ⟹ Y = 2 X 2 − X
Squaring both sides, we have Y 2 = 2 X 2 ( 3 − 2 2 ) .
Finally, the ratio of the areas is Y 2 X 2 = 2 X 2 ( 3 − 2 2 ) X 2 = 3 − 2 2 2 and the desired answer is 2 : 3 − 2 2
If LP= r is the radius of the circle, LR the diagonal of LMRN=
2
r and PR=RL-PL, the diagonal of PQRS = (
2
-1)r.
So the ratio=
{
2
−
1
2
}
2
⟹
2
:
3
−
2
.
The correct answer is 2 : ( 3 − 2 2 )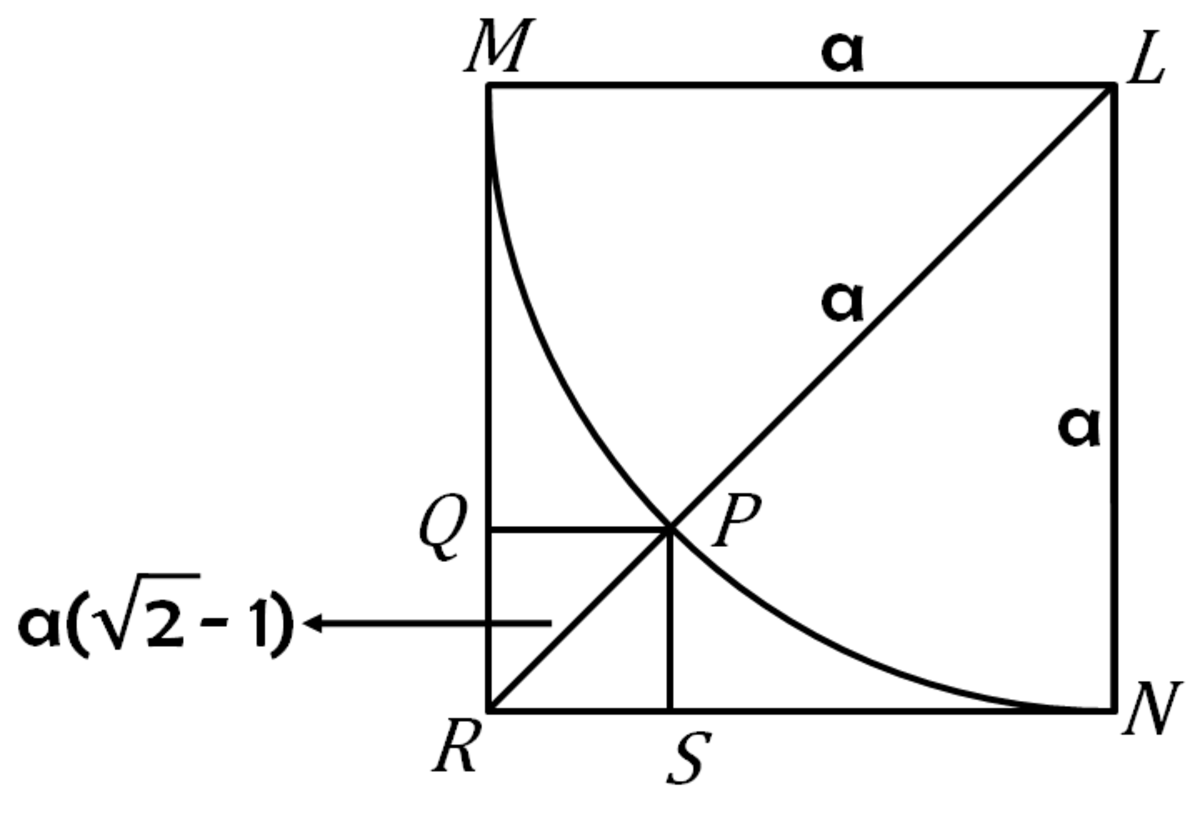 It is given that
R
S
passes through
L
and
R
Q
passes through
M
.
It is given that
R
S
passes through
L
and
R
Q
passes through
M
.
On drawing the line R S L and R Q M , the diagram shown above results. From the diagram, it is clear that M N L R has to be a square and P has to be the mid-point of the arc.
As P is the mid-point of the arc, R N passes through P ,
R P = a ( 2 − 1 )
where M N = P N = a
⇒ P Q = 2 R P
= a ( 2 − 1 ) / 2
M N 2 : P Q 2 = 2 : 3 − 2 2