A geometry problem by Yahia El Haw
Find the area of the regular octagon inscribed in a circle of radius r .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
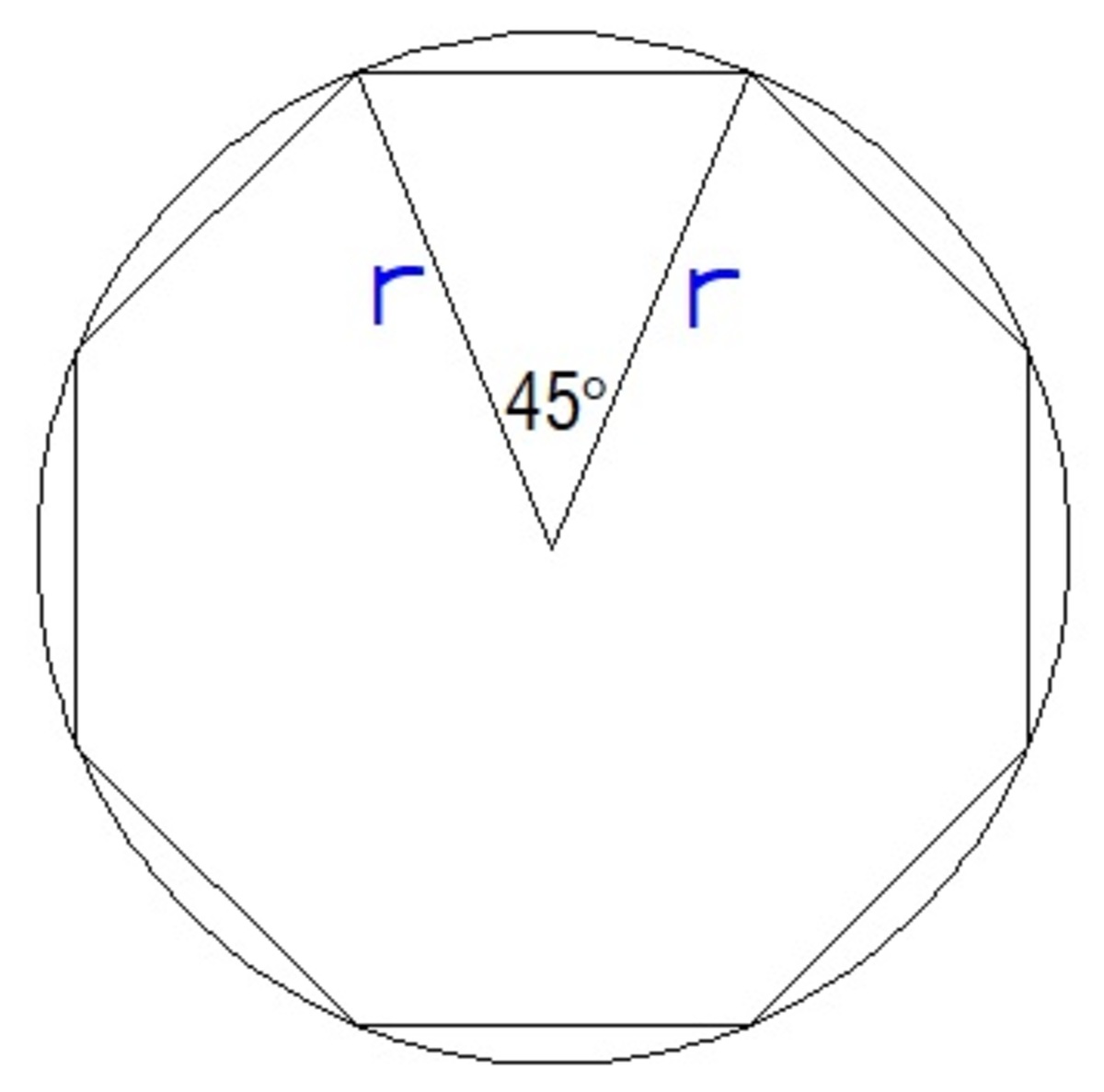 A regular octagon is composed of
8
congruent isosceles triangles. From the diagram, the included angle between the two equal sides is
8
3
6
0
=
4
5
∘
. For the area of the triangle, we use the formula
A
=
2
1
a
b
sin
C
. So the area of the octagon is
8
(
2
1
)
(
r
2
)
(
sin
4
5
)
=
4
r
2
(
2
2
)
=
2
r
2
2
.
A regular octagon is composed of
8
congruent isosceles triangles. From the diagram, the included angle between the two equal sides is
8
3
6
0
=
4
5
∘
. For the area of the triangle, we use the formula
A
=
2
1
a
b
sin
C
. So the area of the octagon is
8
(
2
1
)
(
r
2
)
(
sin
4
5
)
=
4
r
2
(
2
2
)
=
2
r
2
2
.
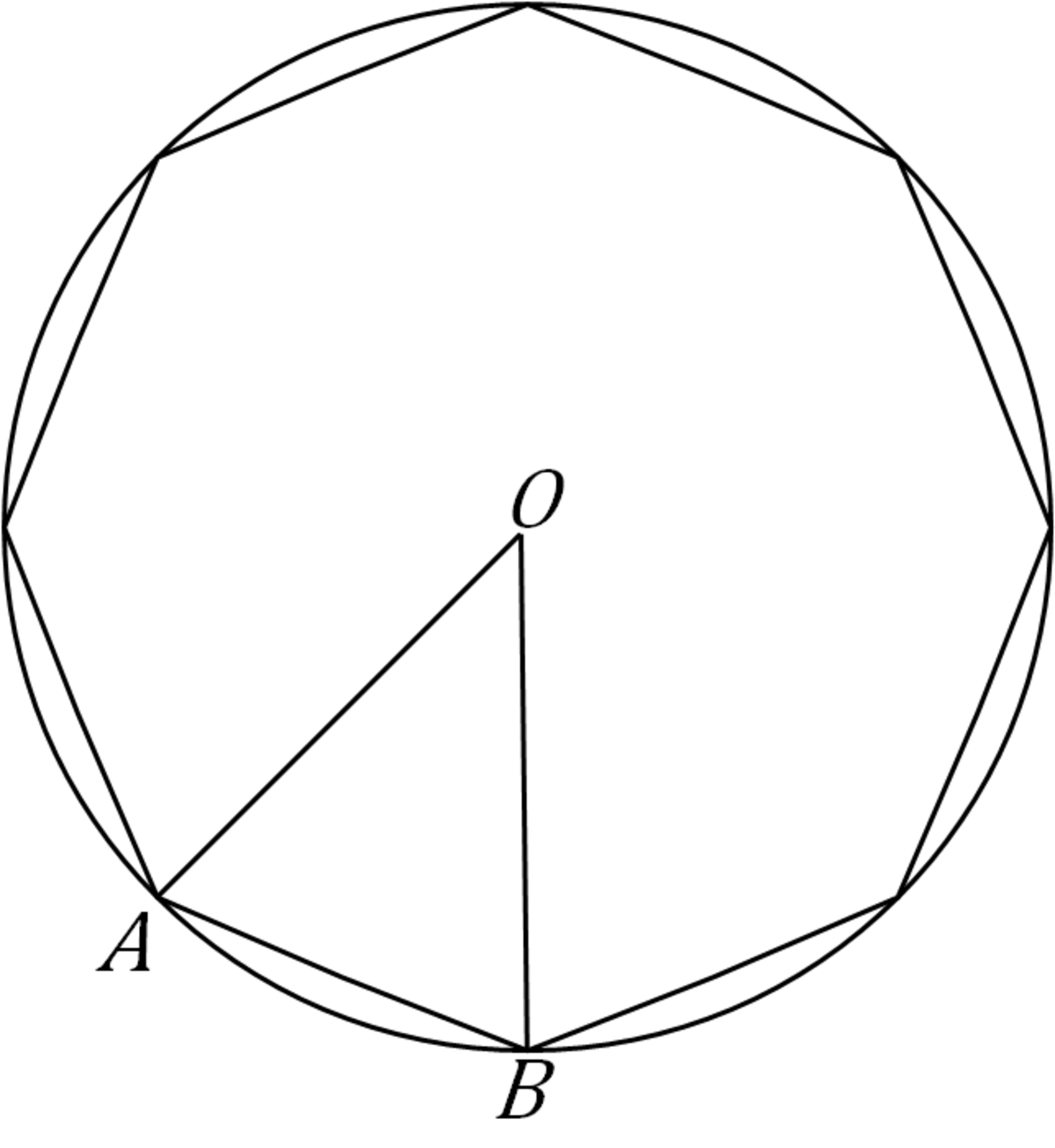 μ
(
A
O
B
)
=
4
π
μ
(
A
O
B
)
=
4
π
σ [ A O B ] = 2 r 2 sin 4 π = 2 r 2 sin 2 2 = 4 r 2 2
σ [ o r t h o g o n ] = 8 ⋅ 4 r 2 2 = 2 2 r 2
The real answer should be (sqrt(8) * r^2), r^2 not being under the surd roof.
Log in to reply
They're equal. 8 r 2 = 2 2 r 2
Log in to reply
My point was not the 8 or 22, but r^2 not having a roof over its head.
I agree with @Saya Suka . The answer, as stated, is only correct for a circle of unit radius.