A Problem from my book-8
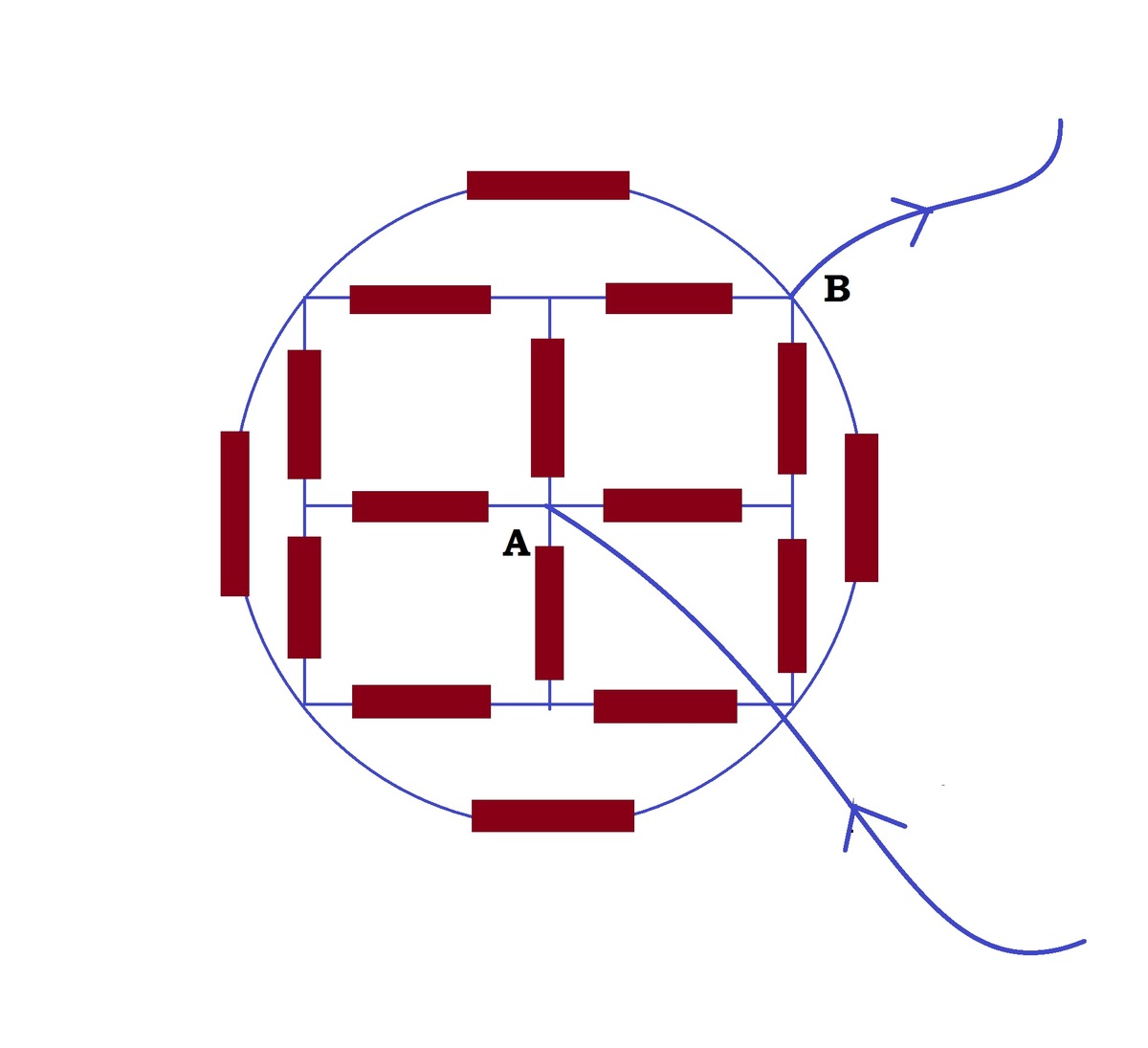
In the circuit above every resistor is 2 . If the equivalent resistance between and is , where and are coprime integers. Find .
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Transformation of Resistances (Star to Delta and Delta to Star)
Although it is possible to use Kirchhoff´s laws to solve for the equivalent resistance, it is much easier to look for resistance conected in series and parallel and progressively reduce the circuit.
Since the the original circuit is symetrical with respect to the diagonal that passes through points A and B, a node from a side of the diagonal is at the same potential as the node that is its reflexion with respect to the diagonal. This could also be thought as follows: a source of potential (like a battery) is connected to points A and B, the current "I" flowing through the resistors immediately connected to point A should be the same, because both resistors have the same resistance and the circuit is symetrical, as shown in the upper-left image. Hence, there is an equal potential difference through these resistors. A similar analysis can be made to the rest of the resistors.
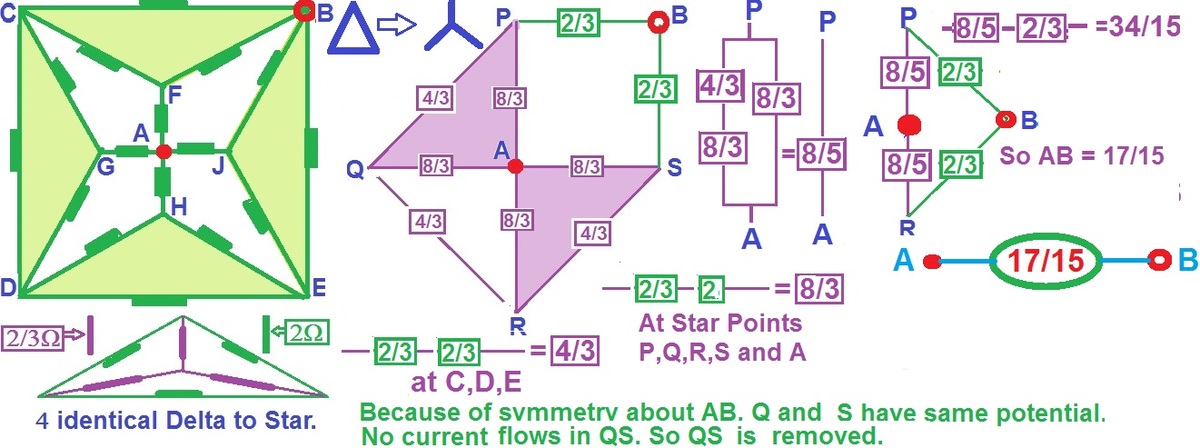
Knowing this, we could look for nodes with the same potential and, hence, resistors with the same potential difference (resistors in parallel). In the upper-centered image, nodes with the same potential have the same color.
The original circuit can be reduced by "combining" the resistors that are in parallel, the resultant circuit is shown in the upper-right image (the resistors in that image are 1 Ω each).
The circuit can be reduced further by "adding" resistors in series and parallel and it can be rearranged into an unbalanced, Wheatstone bridge with a resistor of 3 5 Ω and the other four (including the bridge) of 1 Ω as it is shown by the lower-left and lower-centred images.
The Wheatstone bridge is unbalanced so a current flows through the bridge and the circuit can´t be further reduced unless an equivalent network is used. Such equivalent circuit can be easily found be using an Delta-Star transformation on the three lower resistors (which are arranged in a "delta" shape) of the circuit shown in the lower-centred image.
After the transformation, the circuit shown in the lower-right is obtained, where the three lower resistors are arranged in a "star" shape and are 3 1 Ω each (due to the transformation). This circuit is a "simple" one and the equivalent resistance can be obtained by "combining" the resistors in series and parallel.
From the image: R = ( ( 5 / 3 + 1 / 3 1 + 1 + 1 / 3 1 ) − 1 + 3 1 ) Ω = 1 5 1 7 Ω Where "R" stands for equivalent resistance.
Hence the answer is 17+15=32