A problem of Sequence

Let $b_n = a_{n+1} - a_{n}$ , so $b_1 = 1024 = 2^{10}$ and $b_{n+1} = \frac{1}{2} b_n$ .

$a_{12} = b_{11} + b_{10} + ... + b_2 + b_{1} + a_1 = (\frac{1}{2^{10}} + \frac{1}{2^9} + ... + \frac{1}{2} + 1)*2^{10}) + 705 = (1 + 2^1 + 2^2 +... + 2^9 + 2^{10} + 705 = 2^{11} - 1 + 705 = 2048 - 1 + 705 = 2752.$

Solving the recurrence relation $2a_{n+2} - 3a_{n+1} + a_n = 0$ , we look for solutions of the form $a_n = u^n$ . A solution of this type will work provided that $0 \; = \; 2u^2 - 3u + 1 \; = \; (u-1)(2u-1)$ and hence $u = 1,\tfrac12$ . Thus the general solution of this recurrence relation is $a_n = A + B2^{-n}$ for constants $A,B$ . Matching the initial conditions $a_1=705$ , $a_2=1729$ gives $A=2753$ and $B=-4096$ . Thus $a_n \; = \; 2753 - 2^{12-n} \hspace{2cm} n \ge 1$ and hence $a_{12} = 2753-1 = \boxed{2752}$ .

By visiting the website here and typing the numbers as the picture and you'll get the answer of $\boxed{2752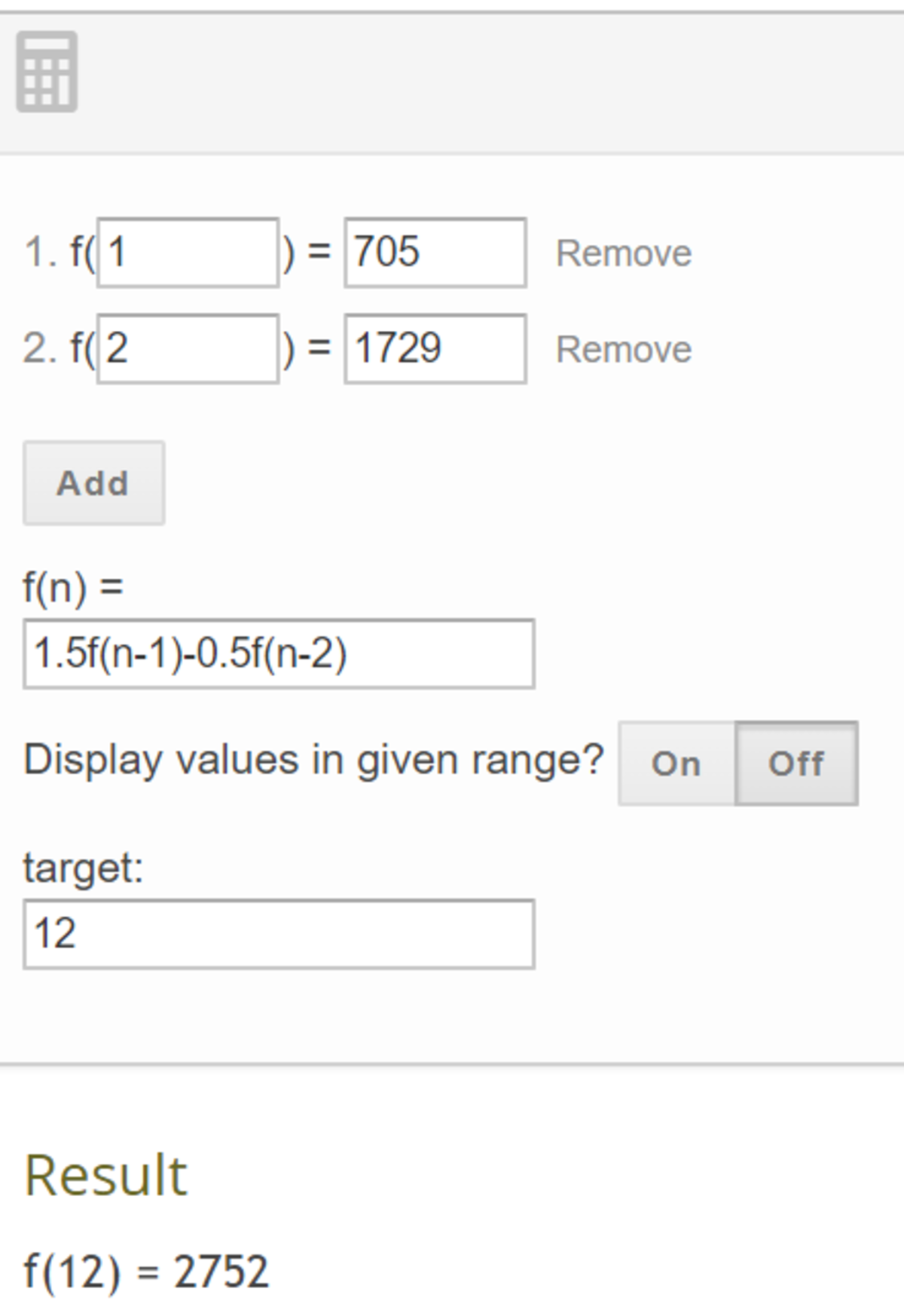}$ The picture