A problem on a simple result
A circle is inscribed in a quadrilateral, as shown above. The two blue sides have lengths 17 and 13, respectively. What is the sum of the lengths of the other two red sides?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
In 3rd line there is a problem it is not DS it is BS thank you...
Regarding the phrasing of the multiple-choice answers: Since all of the choices were integers, it was immediately obvious that the solution was 30 and that there must be a theorem such as Pitot's. If the quadrilateral is a square, then the solution is obvious. But with the arbitrary and nonspecified conditions in your figure (except for the given sum of the two side lengths), the other side lengths, or their sum, are incalculable except in terms of a theorem like Pitot's. Since all the choices were not only exact but integers, none of them could be deduced except in light of such a theorem.
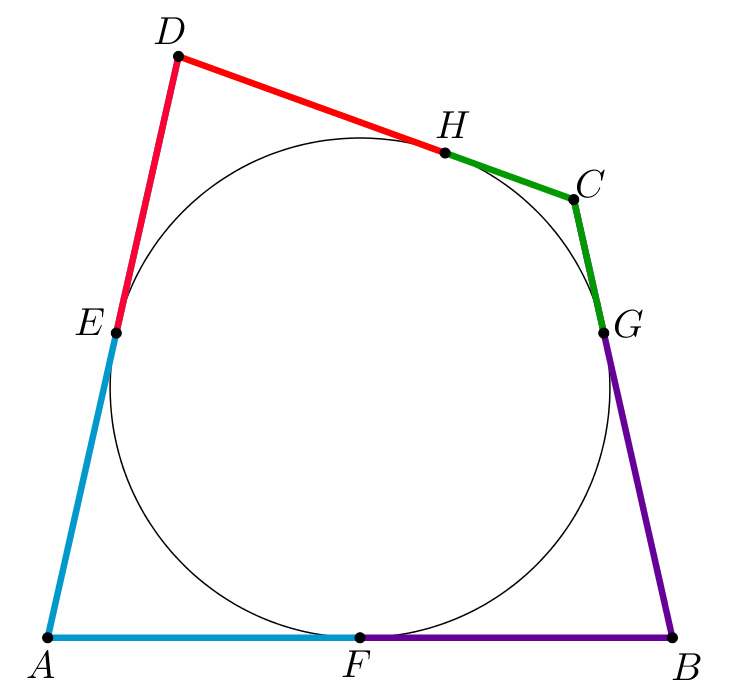
Since A F , F B , B G , G C , C H , H D , D E , A E line segents are tangential, A F = A E , B F = B G , C G = C H , D H = D E . So A D + B C = A E + E D + B G + G C = A F + B F + C H + D H = A B + C D = 3 0 .
Perfect! Can you just add a final statement saying generally speaking AB+CD=AD+BC.
Log in to reply
The result actually has a name: Pitot's Theorem .
Log in to reply
Thank you buddy! I did know of the theorem but did not know a brilliant wiki existed :)
Wow, this is a brilliant way to visualize it!
Great picture!
Pitot thereom says that in a tangential quadrilateral a pair of opposite sides equal the same length as the sum of the other pair of opposite sides. So 17+13=30 thus the sum of the other pair is 30.
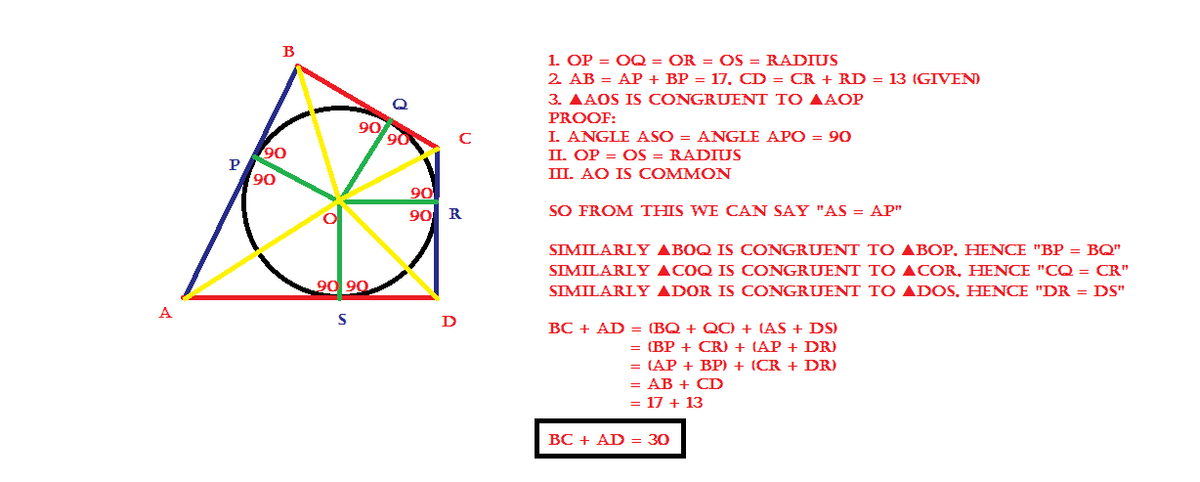
Relevant wiki: Pitot's Theorem
A quadrilateral has an inscribed circle (that is, a circle tangent to each of its sides) if and only if the sums of the lengths of the two pairs of opposite sides are equal. In the above problem, the circle is inscribed in the quadrilateral if and only if the sum of the lengths of the b l u e s i d e s is equal to the sum of the lengths of the r e d s i d e s . Therefore, the sum of the lengths of the r e d s i d e s is 1 7 + 1 3 = 3 0 .
Proof: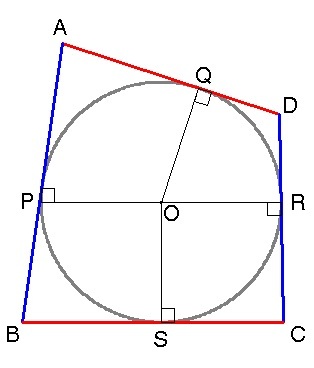 Since the tangents to the circle from an external point have the same length, then
Since the tangents to the circle from an external point have the same length, then
A P = A Q , P B = B S , S C = C R and R D = Q D .
such that
A B + C D = A P + P B + C R + R D
A B + C D = A Q + B S + S C + Q D
A B + C D = ( A Q + Q D ) + ( B S + S C )
A B + C D = A D + B C