A problem on equivalent resistance
Determine the resistance
in ohms
between the points A and B (equivalent resistance) of the circuit shown below. All the values of the resistances are given in ohms.
The answer is 2.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
What is kirchoff's law of tensions
Can't it be done by Ohm's Law?
How do you know its I/2 in the center of the circuit
Transform first and last PI to Y. And you can easily see where is series and parallel.
@Ivan Henrique Petrin : Please, may you please explain how you got the current distribution by symetry? Thank you so much in advance :)
The problem can be readily solved using the wye-delta transformation. Let the top two unlabeled nodes be C and D from left to right and the bottom two, E and F . The left 1-2-3 Ω delta is transformed to R a = 2 1 Ω , R c = 1 Ω , and R e = 3 1 Ω . Similarly, for the right delta, R b = 2 1 Ω , R d = 1 Ω , and R f = 3 1 Ω .
The resultant resistance between A and B :
R a b = R a + ( R c + 2 + R d ) ∣ ∣ ( R e + 2 + R f ) + R b = 2 1 + ( 3 1 0 ∣ ∣ 3 1 0 ) + 2 1 = 2 1 + 3 5 + 2 1 = 3 8 ≈ 2 . 7 Ω
I have solved this using delta star conversion.... But its very lengthy...
Would you provide a picture after the transformation?
The 1, 2 and 3 ohm resistors on both sides are delta connected. Convert it to wye connection. R13 = (1)(3)/(1+2+3) R12 = (1)(2)/(1+2+3) R23 = (2)(3)/(1+2+3)
Then. R12 from side A, R23 from side B and the 2 ohm resistor in the middle is series. And same as the resistances below. Since they are connected in parallel and their resistances are the same, divide it by 2 to get its resistance equivalent.
Finally, those remained are series, 0.5 + 1.66666666667 + 0.5 = 2.66666667 or 2.7 ohms.
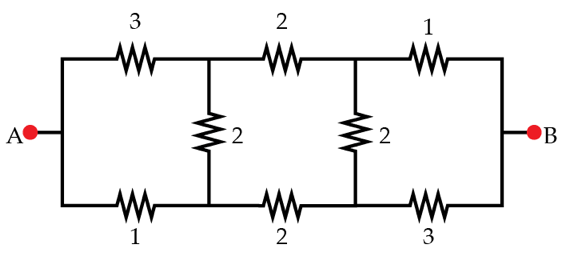
i found other solutions so tedious so i'll upload an easy one, connect a 100 volt battery(for ease of calculations)
assume potientals to be x and y and then using symmetry for potential drop solve for x and y use ohm's law and the calculate
notice that the end meshes look like DELTA configurations...hence they can be converted to the corresponding STAR configurations and then simplify and get the answer as 2.6667 ohm.
can u pls xplain me DELTA config??
it's called wheatstone bridge, google it...
Log in to reply
an "unbalanced" Wheatstone bridge ....to be precise....
I converted the 2 delta circuits at both ends to be Y-circuits, then ended up with a series-parallel-series circuit...
application of delta-to-star conversion..simple
The electrical circuit diagram in this problem can be transformed by using Y- Δ transformation technique . After transformation, we can calculate the equivalent resistance between A and B by using basic series and parallel resistors configuration.
# Q . E . D . #
Solultion is 2.7 ohm
We can get the equivalent resistance of a circuit by connecting an ideal source of tension and measuring the current that pass through the source.
By the simmetry of the problem we would get the distribution of currents shown in the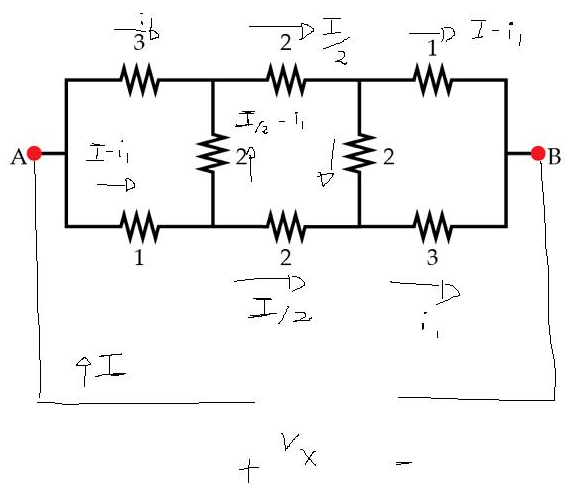 (sorry for the quality)
(sorry for the quality)
By using Kirchoff Law of Tensions following the path shown below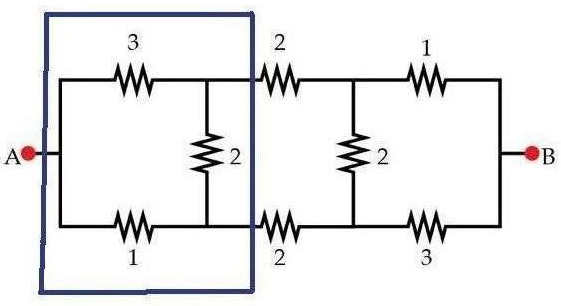
and then going though the source and doing this path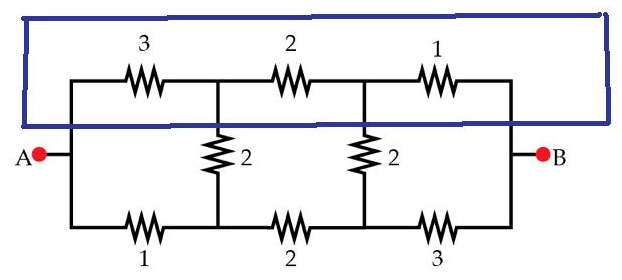
we obtain the following equations:
3 i i − 2 ( − i 1 + 2 I ) − ( I − i 1 ) = 0
V x = 3 i 1 + 2 2 I + I − i 1
By solving the first one we get i 1 = 3 I
Using this in the second we get V x = 3 8 I = > I V x = 3 8
So the equivalent resistance is R = 3 8 Ω