Orthocentre,Circumcentre and two other points

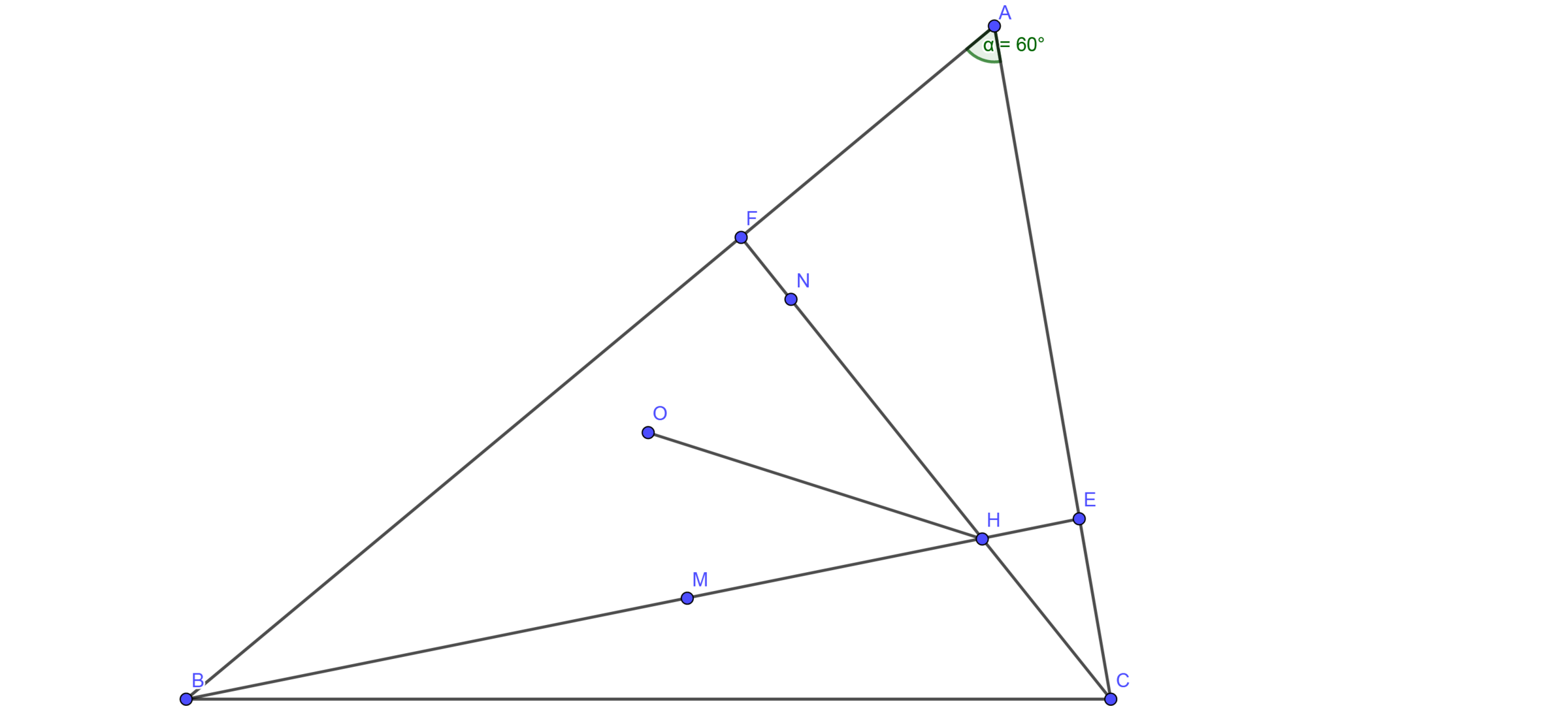
In the figure above, $\bigtriangleup ABC$ is a triangle in which $\angle A=60^{\circ}$ , $\overline{AB}>\overline{AC}$ , point $O$ is the circumcentre and $H$ is the orthocentre. Points $M$ and $N$ are on the line segments $\overline{BH}$ and $\overline{HF}$ respectively such that $\overline{BM} = \overline{CN}$ .

Determine the value of $\dfrac{MH+NH}{OH}$ .

Bonus: Solve without using trigonometry and coordinate geometry.

This problem is not created by me.