A problem redone (because the last one was too easy)

Logic Level 4

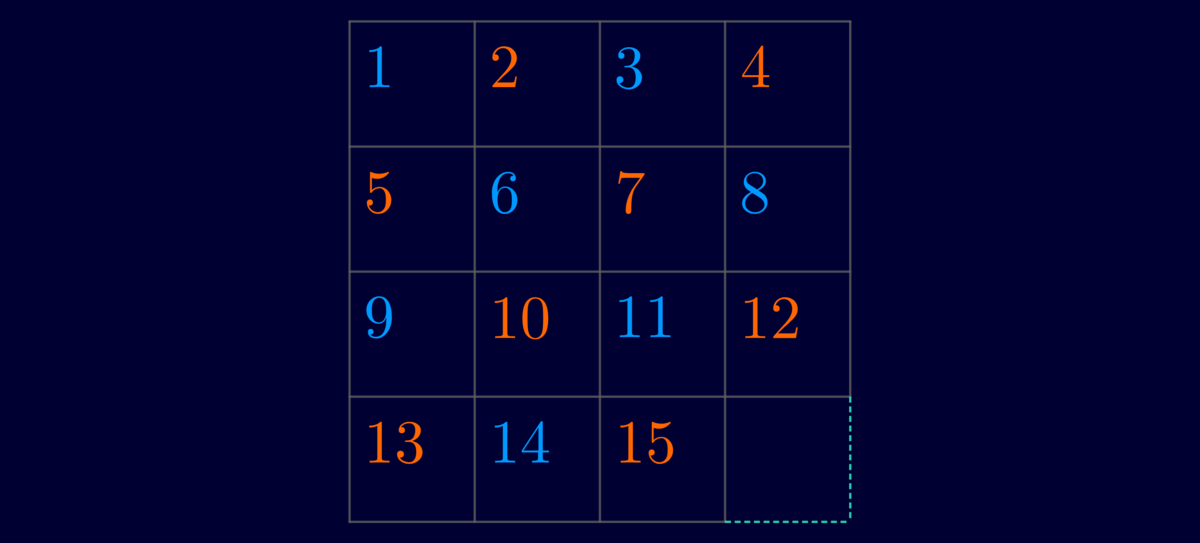
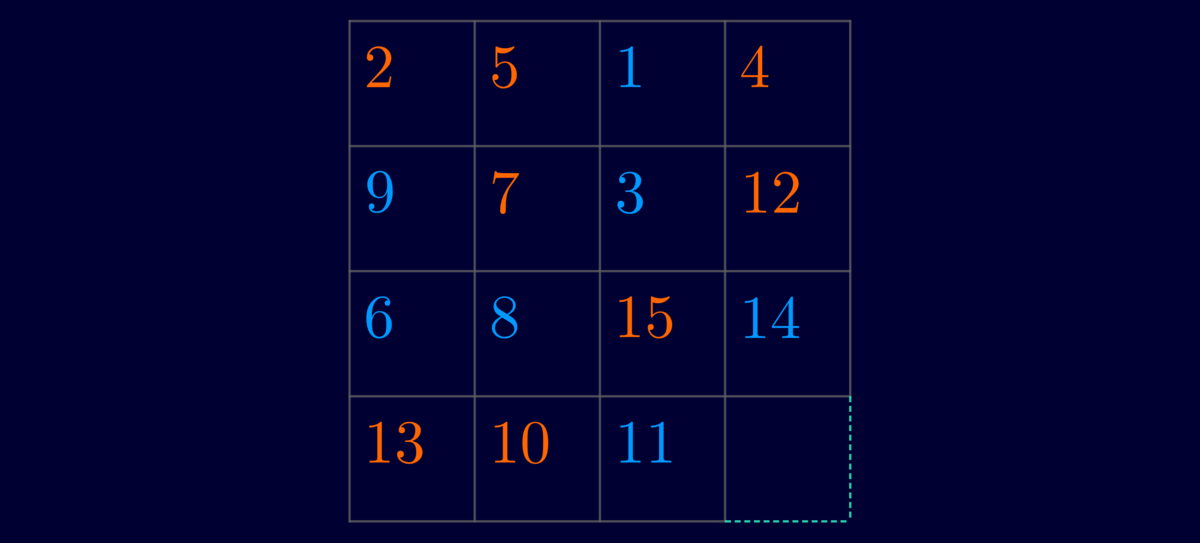
What is the minimum amount of moves to transform from the above square to the below square?

Note:

A move is moving 1, 2 or 3 squares of the same row or column - which has one empty square - one square up, right, down or left without changing the original order of the squares that are moved. (Basically, you slide those squares.)

13 8 9 10 15 14 12 11

1 solution

K T
Jul 29, 2019

Did some brute force. Note that from each position, there are only 3 horizontal moves and 3 vertical moves. And performing two horizontal or two vertical moves in row is sub optimal, so for a sequence of 15 moves there are 2×3^15=28 million possibilities. This should be within reach of brute force. Here is the code, that finds the (a) shortest solution and prints its steps:

def StartPosition():
    global A, X, Y;
    X=3; # position of the 0
    Y=3;
    A=[[2,9,6,13],[5,7,8,10],[1,3,15,11],[4,12,14,0]];

def MoveHor(NewX):
    global X;
    for X_ in range(X, NewX): # NewX>X, hole moves to the right, blocks to the left
        A[X_][Y] = A[X_+1][Y];
    for X_ in range(X, NewX, -1): # NewX<X, hole moves to the left, blocks shift to the right
        A[X_][Y] = A[X_-1][Y];
    X = NewX;
    A[X][Y] = 0;

def MoveVer(NewY):
    global Y;
    for Y_ in range(Y, NewY):
        A[X][Y_] = A[X][Y_+1];
    for Y_ in range(Y, NewY, -1): 
        A[X][Y_] = A[X][Y_-1];
    Y = NewY;
    A[X][Y] = 0;

def printA():
    for y in range(0,4):
        for x in range(0,4):
            print (" {:2}".format(A[x][y]), end = '');
        print();
    print();

def check():
    for y in range(0,4):
        for x in range(0,4):
            if A[x][y]!=(4*y+x+1)%16:
                return False;
    return True;

def iterateHorVer(depth):
    oldX=X;
    oldY=Y;
    global MoveList;

    if depth==0:
        return check();

    for xx in range(0,4):
        if xx==oldX:
            continue;
        MoveHor(xx);

        if check():
            MoveList.insert(0,xx);
            return True;

        if (depth>=2):
            for yy in range(0,4):
                if yy==oldY:
                    continue;
                MoveVer(yy);
                result=iterateHorVer(depth-2);
                if result:
                    MoveList.insert(0,yy);
                    MoveList.insert(0,xx);
                    return True;
        #restore original y position
        MoveVer(oldY);
    #restore original x position
    MoveHor(oldX);
    return False;

StartPosition();
MoveList=[];

print("starting from");
printA();

for i in range(0, 20, 2):
    if result:
        continue;
    print("Trying a horizontal move first in max. {} moves...".format(i));
    HorizontalFirst=True;
    result= iterateHorVer(i);
    if result:
        continue;

    print("Trying a vertical move first in max. {} moves...".format(i+1));
    HorizontalFirst=False;
    for j in range (0,4): 
        if j==Y or result:
            continue;
        #print(j, X, Y);
        #printA();
        MoveVer(j);
        if iterateHorVer(i):
            MoveList.insert(0,j);
            result=True;

if result:
    print ("Found a solution in {} moves, starting {}: ({}).".format(
        len(MoveList), 
        "horizontally" if HorizontalFirst else "vertically",
        ', '.join(str(M) for M in MoveList)
    ));

    StartPosition();

    print("Solution steps:");
    for M in MoveList:
        if HorizontalFirst:
            MoveHor(M);
        else:
            MoveVer(M);
        printA();
        HorizontalFirst = not HorizontalFirst;

A problem redone (because the last one was too easy)

1 solution

0 pending reports