A Problem with RNGs
Computers are really bad at random number generation. Really bad. I've encrypted 2 images, shown below, with python's random module (Hint, it uses MT19937). The first, smaller image is named
flag_enc.png
and the other image is named
original_enc.png
.
-
flag_enc.png: flag_enc.png -
original_enc.png: original_enc.png
Note, the above files are no longer valid PNGs since they have been encrypted.
Here is the source code that was used to encrypt the files:
1 2 3 4 5 6 7 8 9 10 |
|
In addition, you are given that
original.png
is the following image:
Here
Recover
flag.png
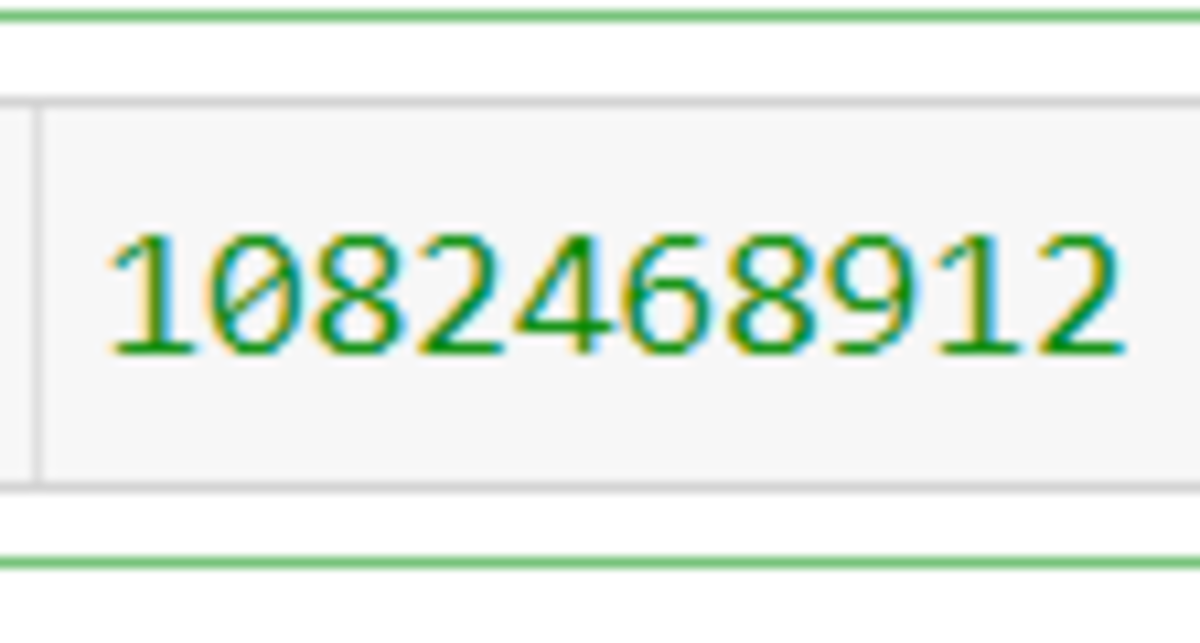
and write the number in the image as your answer.
The answer is 1082468912.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Python's
randommodule uses MT19937 to generate its numbers. How MT19937 works is that it is essentially a huge xor machine. In other words, the RNG has an internal state that contains 1 9 9 6 8 bits, and it generates it's numbers by a sequence of XOR of it's state. This means that given enough numbers that it generates, it is possible to solve for the internal state. The internal state can then be used to "clone" the RNG simply from the knowing the numbers it produces!XOR of 2 bits is essentially an addition done mod 2. This means that the generated numbers of an MT19937 can be described with a matrix M where the generated numbers G are G = M I where I is the internal state of the MT19937. This enables us to simply solve for I via Gaussian Elimination.
However, the internal state that we clone from
original.pngandoriginal_enc.pnghas been forwarded 8 8 9 times, the number of bytes inflag.png, since the source code encryptedflag.pngfirst. This means, we have to reverse the RNG state 8 8 9 times. Since MT19937 is a huge xor machine, we can use Gaussian Elimination reverse the RNG the desired number of times.My code for the above steps are in the Github Repo MT19937-Symbolic-Execution-and-Solver and below is my code to solve this problem, and the decrypted image.