A proton beam hitting a target
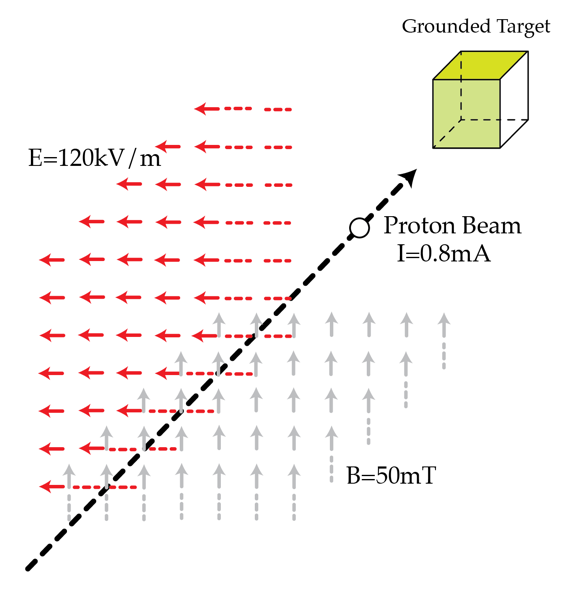
A non-relativistic proton beam passes without deflection through a region where there are two transverse, mutually perpendicular, electric ( E = 1 2 0 kV/m ) and magnetic ( B = 5 0 mT ) fields. Then the beam strikes a grounded target. Find the force in Newtons with which the beam acts on the target if the beam current is I = 0 . 8 mA . Assume that the collisions with the target are inelastic.
Details and assumptions
The proton's mass and charge are: m p = 1 . 6 7 × 1 0 − 2 7 kg e = 1 . 6 × 1 0 − 1 9 C .
The answer is 0.00002.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
the velocity of the proton beam is given by v=E/B. The force acting on the grounded target is given by F=dp/dt=(N A m dx v)/dt=NAmv^2 where N is the number density of proton. Furthermore,I=dq/dt= (N A e*dx)/dt=NAev^2.By substituting the expression for v and NA into equation F=dp/dt, we can get the value of F=2 x 10^-5
as beam not deflected electric and magnetic forces cancel each other
E e=B e*v
or E=v*B
let n number of protons flowing per second
n*e=i
F=rate of change of momentum(force)
F=v*(dm/dt) (as only mass changes and velocity is constant)
dm/dt=n*(mass of each proton)
substituting the values we get the result F=2.004*10^-5
In a cross E-B field,if there is no deflection of a charge then, velocity, V=E/B Force, F=dP/dT
Now,in time dT ,Charge which came to rest, dQ=IdT
Protons stopped, n=(IdT)/e
Mass which came to rest, dm=n*m
Momentum Change,
dP=Vdm
or dP=(E/B) (IdT/e) (m)
or dP/dT=(E I m)/(B*e) (Putting the values)
or F=2.004E-5 Newton
Despite the presence of 2 fields directing the proton beam to opposing directions, the question states that the beam passes with no deflection. This indicates that the force due to the magnetic field and the electric field (as well as the motion of the protons), balances each other completely.
Force due to electric field: F(e)=qE=1.6E-19 * 120E3 = 1.92E-14
Force due to magnetic field: F(B)=qvB=1.6E-19 * v * 50E-3 = 8E-21 v
Equating the two, we get v = 2.4E6
Now, given I, we can find the time, t , for the passing of each proton. t = Q/I = 1.6E-19 / 0.8E-3 = 2E-16
Finally, force, F. F= ma = m Dv/Dt = (1.67E-27 * 2.4E6)/(2E-16) = 2.00E-5
The beam is not deflected by the fields if the Lorentz force is zero. This implies F = e ( E + v × B ) = 0 . Since the fields are mutually perpendicular, the above condition can be simply written as v = B E which yields the velocity of protons. Now, by definition the current I is proportional to the number of protons hitting the target per unit time Δ t Δ N . More precisely, I = e Δ t Δ N . On the other hand, the force acting on the target is F = Δ t Δ p = m p v Δ t Δ N where m p is the mass of the proton. Note that in the last equation we made use of the fact that the collisions are inelastic. Putting the above equations together we find the force F = e m p B E I = 2 × 1 0 − 5 N .
The electric force ( eE ) acting on a proton is directed to the left. The magnetic force ( evB ) acting on a proton is directed to the right. These forces cancel out ( eE - evB = 0 ), therefore, v = E / B . Suppose that n protons hit the target in a time t . Hence, I = ne / t , therefore, I / e = n / t . It is assumed that the protons are at rest after collision. The impulse delivered by the beam in a time t , is equal to the momentum of n protons ( Ft = nmv ). Therefore, F = (n / t) mv . The final expression is: F = ImE / (eB) . Substituting given values yields, F = 2 × 1 0 − 5 N .