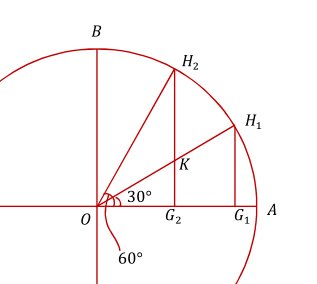
A quarter circle

Geometry Level 1

O A B OAB is a quarter circle, and points H 1 H_1 and H 2 H_2 divide the arc into three equal parts. Now, we drop perpendiculars from H 1 H_1 and H 2 H_2 to O A OA .

Which is larger, the blue triangle or orange quadrilateral?

Blue triangle Orange quadrilateral They are equal

View wiki
Áron Bán-Szabó by Áron Bán-Szabó , 17, Hungary

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

This is a proof without words solution:

7 Helpful 0 Interesting 0 Brilliant 0 Confused
Marta Reece
Jun 8, 2017

T = [ O H 1 G 1 ] − [ O K G 2 ] T=[OH_1G_1]-[OKG_2]

t = [ O H 2 G 2 ] − [ O K G 2 ] t=[OH_2G_2]-[OKG_2]

T − t = [ O H 1 G 1 ] − [ O H 2 G 2 ] T-t=[OH_1G_1]- [OH_2G_2]

[ O H 1 G 1 ] = 1 2 sin ⁡ 3 0 ∘ cos ⁡ 3 0 ∘ O B ‾ 2 = 3 8 O B ‾ 2 [OH_1G_1]= \frac12\sin30^\circ\cos30^\circ\overline{OB}^2=\dfrac{\sqrt{3}}{8}\overline{OB}^2

[ O H 2 G 2 ] = 1 2 sin ⁡ 6 0 ∘ cos ⁡ 6 0 ∘ O B ‾ 2 = 3 8 O B ‾ 2 [OH_2G_2]= \frac12\sin60^\circ\cos60^\circ\overline{OB}^2=\dfrac{\sqrt{3}}{8}\overline{OB}^2

T − t = [ O H 1 G 1 ] − [ O H 2 G 2 ] = 0 T-t=[OH_1G_1]- [OH_2G_2]=\boxed{0}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...