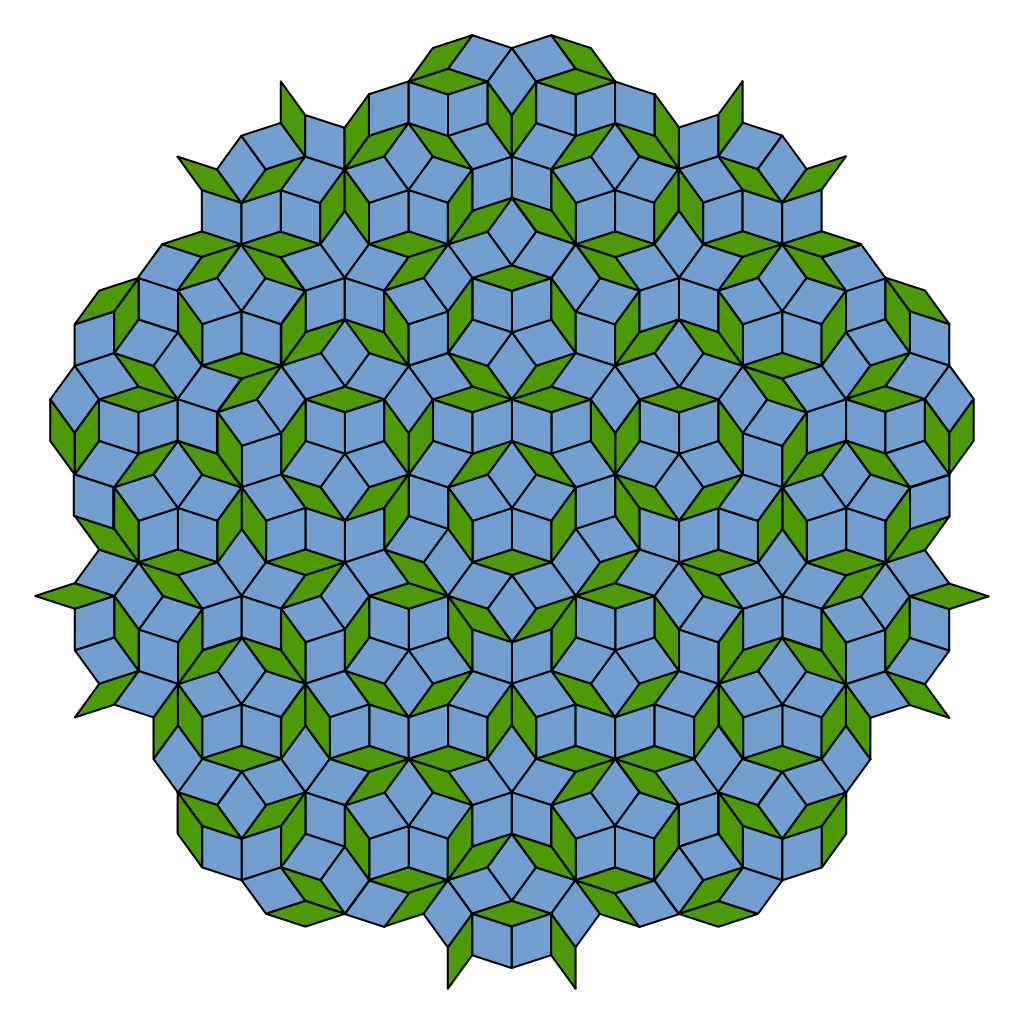
A question about Penrose Euclidean plane tiling.
This problem's question: Why is this statement about Penrose tiling : "Penrose tiling is non-periodic, which means that it lacks any translational symmetry" correct?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are multiple types of aperiodic tilings.
There are tilings that are periodic: e.g., rectangles, triangles and hexagons.
The statement is correct. Mathematical proofs exist to support the statement.
The square root of 5 is used in the construction of the tiles' design. The aperiodicity comes from the fact that other apparent duplicates are subtly rotated from the other apparent copies by the irrational nature of the square of 5.
It is well-known that GoldenRatio, 2 5 − 1 is pervasive throughout the construction of the regular pentagon.