A question on trigonometry

Geometry Level pending

If 0 ∘ < θ < 9 0 ∘ 0^\circ < \theta < 90^\circ and csc ⁡ θ = 13 12 \csc \theta = \dfrac{13}{12} , find 2 sin ⁡ θ − 3 cos ⁡ θ 4 sin ⁡ θ − 9 cos ⁡ θ \dfrac{2\sin \theta - 3\cos \theta}{4\sin \theta - 9\cos \theta} .


The answer is 3.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chew-Seong Cheong
Dec 15, 2020

Given that csc ⁡ θ = 13 12 = 1 sin ⁡ θ ⟹ sin ⁡ θ = 12 13 \csc \theta = \dfrac {13}{12} = \dfrac 1{\sin \theta} \implies \sin \theta = \dfrac {12}{13} . Since cos ⁡ θ = 1 − sin ⁡ 2 θ = 1 − 1 2 2 1 3 2 = 169 + 144 169 = 25 169 = 5 13 \cos \theta = \sqrt{1-\sin^2 \theta} = \sqrt{1-\dfrac {12^2}{13^2}} = \sqrt{\dfrac {169+144}{169}} = \sqrt{\dfrac {25}{169}} = \dfrac 5{13} . Then we have:

2 sin ⁡ θ − 3 cos ⁡ θ 4 sin ⁡ θ − 9 cos ⁡ θ = 2 ( 12 ) − 3 ( 5 ) 4 ( 12 ) − 9 ( 5 ) = 24 − 15 48 − 45 = 9 3 = 3 \frac {2\sin \theta - 3\cos \theta}{4\sin \theta - 9\cos \theta} = \frac {2(12)-3(5)}{4(12)-9(5)} = \frac {24-15}{48-45} = \frac 93 = \boxed 3

4 Helpful 1 Interesting 2 Brilliant 1 Confused

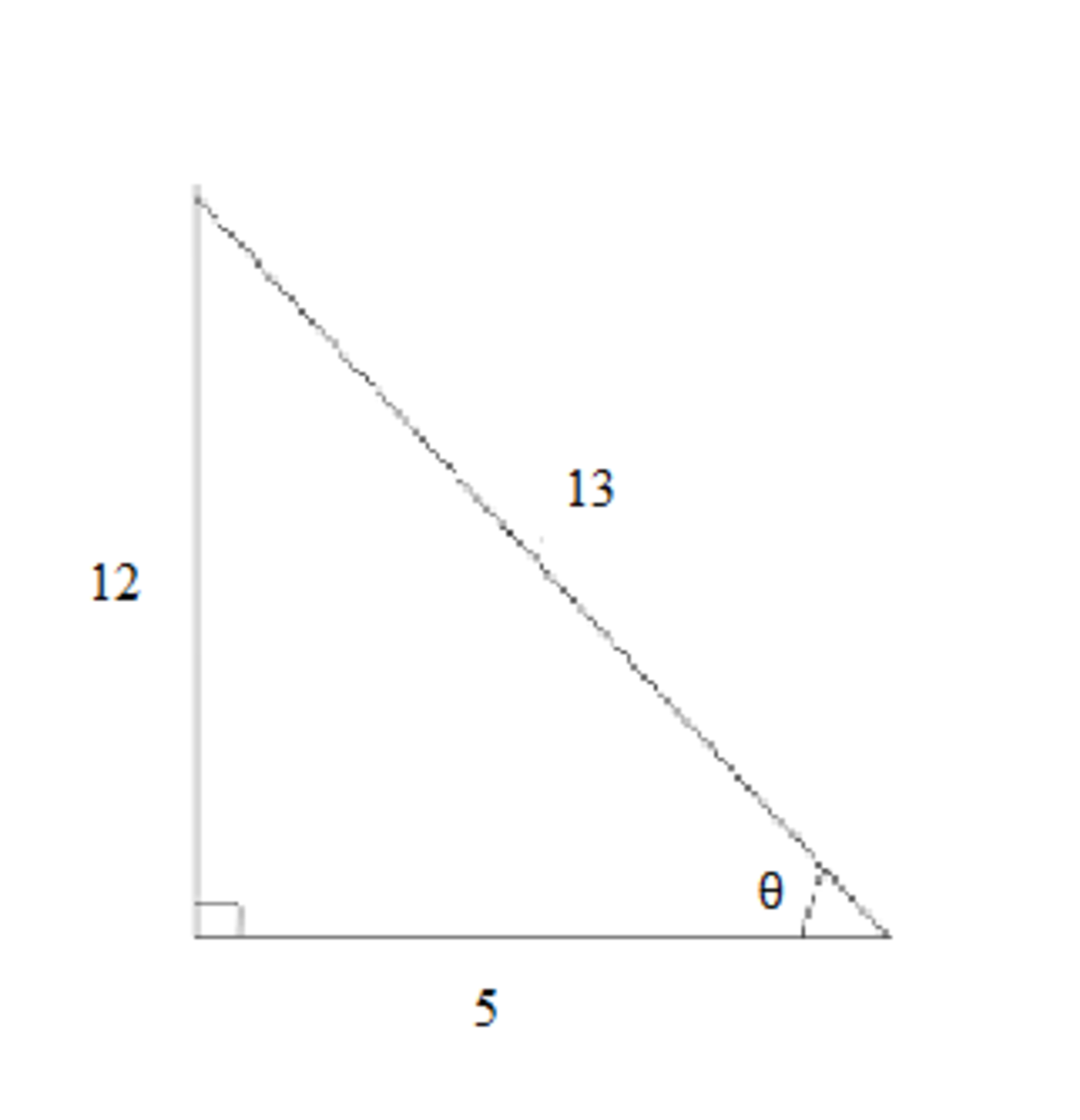
We know that sinθ = o p p o s i t e s i d e h y p o t e n u s e \frac{opposite side}{hypotenuse} and cosθ = a d j a c e n t s i d e h y p o t e n u s e \frac{adjacent side}{hypotenuse} . From this diagram,

sinθ = 12 13 \frac{12}{13} cosθ = 5 13 \frac{5}{13}

From this, 2. s i n θ − 3. c o s θ 4. s i n θ − 9. c o s θ \frac{2.sinθ - 3.cosθ }{4.sinθ - 9.cosθ} can be simplified as 3 \boxed{3}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Nitpick: you have not constrained 0 < θ < π 2 0 < \theta < \frac{\pi}{2} . It could be the case that cos ⁡ ( θ ) = − 5 13 \cos(\theta) = \frac{-5}{13}

Richard Desper - 5 months, 4 weeks ago

Sorry, I forgot that.

A Former Brilliant Member - 5 months, 4 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...