A Quick Triangle Problem
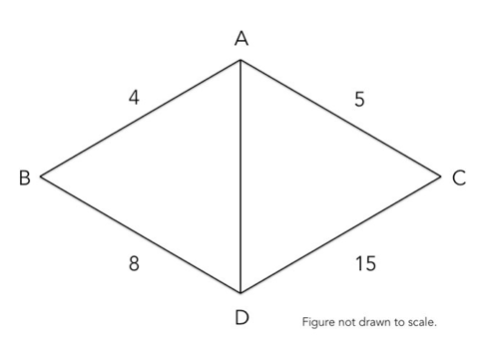
If A B = 4 , A C = 5 , B D = 8 , C D = 1 5 , and A D is a positive integer, find A D .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
@Cody Johnson Thanks for the help
sum of the two sides of a triangle must be greater than the third side:
in this case- AD<(8+4)<(5+15) AD<12<20 so AD<12
now, [as the sides are integer] when AD belongs to (1-10) : triangle ABD and triangle ACD cannot be formed.
when AD = 12
then triangle ABD cannot be formed.
so we are left with only one choice AD = 11
How between 1-10 we cant form triangle will you please explain me?
Log in to reply
it is because (AC+AD should be greater than 15) reason being sum of two sides is always greater than the third side implying that -> 5+AD>15 or AD> 10 so (1-10) wont fit in . I think this may help you
In Triangle ABD, AD less than 12, But in Triangle ADC, AD is greater than 10, So 11 is the answer.
Triangle inequality: 8 - 4 < AD < 8 + 4 15 - 5 < AD < 15 + 5 4 < AD < 12 10 < AD < 20 Only AD = 11 works.
From △ A B D , 4 < A D < 1 2 , but from △ A D C , 1 0 < A D < 2 0 . Thus, A D = 1 1 .
By the triangle inequality, A C + A D > C D , so 5 + A D > 1 5 or A D > 1 0 . But, A B + B D > A D , so 4 + 8 = 1 2 > A D . Therefore, 1 0 < A D < 1 2 , and the only integer satisfying this is A D = 1 1 .