A Radioactive Problem

$\quad \quad \quad \Delta m{ c }^{ 2 }\cdot { n }_{ plutonium }\quad =\quad nF{ E }_{ cell }^{ o }\cdot { n }_{ zinc }\\ \Rightarrow \quad \qquad \qquad \qquad A\quad =\quad (2)(96500)(1.1)\frac { B }{ 65.4 } \\ \Rightarrow \qquad \qquad \frac { A }{ 1000B } =\quad \frac { (2)(96500)(1.1) }{ (65.4)(1000) }$

I don't think it can be simpler.

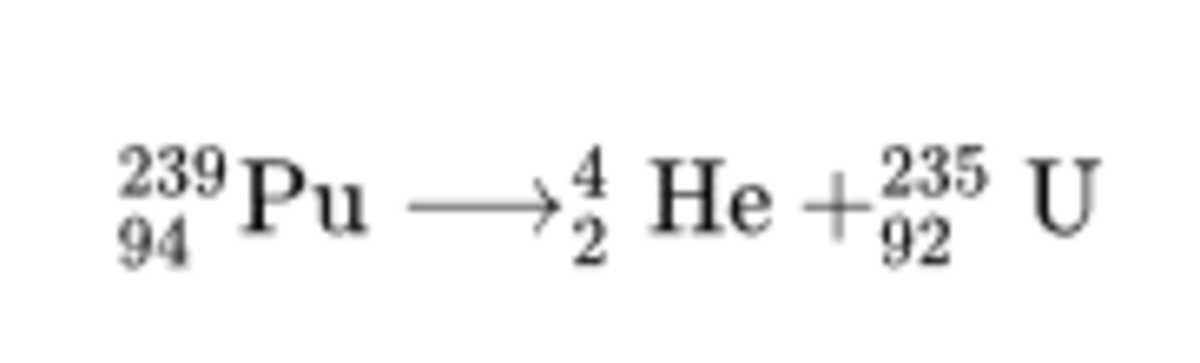delta m = ( mass Pu) - (mass U + mass H) delta m = (239.0006) - (234.9935 + 4.0015) delta m = 0.0056 u/atom

/u = 1.66x10^-24 gram/u mass defeat = 0.0056 u/atom x 1,66e27 kg/u mass defeat = 8.96e30 kg/atom

mol plutonium = 0.215 gram / 239.0006 g/mol mol plutonium = 0.001 mol

atom plutonium = mol x B.Avogadro atom plutonium = 0.001 x 6.02e23 atom plutonium = 602000000000000000000 atom

mass total = 602000000000000000000 atom x 8.96e30 kg/atom mass total = 5.39e-9 kg

E = mc^2 E = 5.39e-9 kg x (3e8)^2 E = 480600000 joule (A)

to obtain the same amount of electrical energy = 480600000 joule 1,10 volt = 1,10 J/C mass Zn = 480600000 joule x (1C / 1,1 Joule) x (1 mol e / 96500 C) (1 mol Zn / 2mol e) (65.39 gram mol Zn / 1 mol Zn) mass Zn = 148028.443 gram (B)

A/B = 480600000 / 148028.443 = 3246.673

The energy obtained from the nuclear reaction $\ce{_94^239Pu -> _2^4He + _92^235U}$ is from the missing mass of the reaction. The energy available from one atomic mass unit $u$ by Einstein's equation $E=mc^2$ (where $c$ is the speed of light in free space) is $E = uc^2$ J. The missing mass due to the decay of a Pu-239 atom is $A_{r(Pu)}-A_{r(He)}-A_{r(U)}$ $= 239.0006 - 4.0015 - 234.9935$ $= 0.0056 u$ . The energy obtained from the delay of $1$ mol of Pu-239 is $E_{mol} = 0.0056 N_A u c^2$ J, where $N_A$ is the Avogadro constant. Therefore, that from $215$ mg of Pu-239 is:

$\begin{aligned} A & = \frac{0.215}{239.0006} \times 0.0056 \color{#3D99F6}{N_A} \color{#D61F06}{u} \color{#20A900}{c}^2 \\ & = \frac{0.215}{239.0006} \times 0.0056 \times \color{#3D99F6}{6.02214 \times 10^{23}} \times \color{#D61F06}{1.66054 \times 10^{-27}} \times \left(\color{#20A900}{2.99792 \times 10^8 }\right)^2 \\ & = 4.52760 \times 10^8 \text{ J} \end{aligned}$

The electrical energy available from $n$ mol of electrons is $E_V = nN_AeE_{cell}^\circ$ J, where $e = 1.60218 \times 10^{-19}$ C is the electron charge. Putting $E_V = A$ , we have $nN_AeE_{cell}^\circ = 4.52760 \times 10^8 \quad \Rightarrow n = \frac{4.52760 \times 10^8}{N_AeE_{cell}^\circ}$ . Since each mol ( $65.38$ g) of $\ce{Zn}$ gives two mol of electrons, then:

$\begin{aligned} B & = \frac{n}{2} \times 65.38 \\ & = \frac{4.52760 \times 10^8 \times 65.38}{2 \times 6.02214 \times 10^{23} \times 1.60218 \times 10^{-19} \times 1.1} \\ & = 1.39453 \times 10^5 \text{ g} \end{aligned}$

$\Rightarrow \dfrac{A}{1000B} = \dfrac{4.52760 \times 10^8}{1.39453 \times 10^8} = 3.24668 \approx \boxed{3}$

.

Applying notation of 1E+4 = 1 $\times 10^4:$

Before (g/ mol): 239.0006

After (g/ mol): 4.0015 + 234.9935 = 238.995

Lost of mass per mole (kg/ mol) = (239.0006 - 238.995)/ 1000 = 5.6E-06

Number of mole of $_{94} ^{239} Pu = \frac{0.215}{239.0006}$ = 8.99579331600004E-04

Speed of light, c (m/ s) = 299792458

Only way available is to apply $E = m c^2$ = 8.99579331600004E-04 $\times$ 5.6E-06 $\times$ 299792458 $^2$ = 4.52760886456606E+08 J = $A$

http://hyperphysics.phy-astr.gsu.edu/hbase/chemical/electrochem.html

$E_{cell} = 1.1 V$

Faraday constant = 96485.33289 Columbs/ mol

Number of mole of $e^-$ required = $\frac{Energy}{Faraday~constant \times E_{cell}} = \frac{4.52760886456606E+08}{96485.33289 \times 1.1}$ $= 4.26594170886984E+03$

Number of mole of $Zn^{2+}$ required = $\frac{4.26594170886984E+03}{2} = 2.13297085443492E+03$

Mass of Zn required = 2.13297085443492E+03 mol $\times$ $65.38 g/ mol$ = 1.39453634462955E+05 g = $B$

$\lfloor \frac{A}{1000 B} \rfloor$ = $\lfloor \frac{4.52760886456606E+08}{1.39453634462955E+08} \rfloor$ = $\lfloor 3.24667684854696 \rfloor$ = 3 (Also equals to value rounded to the nearest integer.)

$Caution:$ It was stated in a book that "the change in mass is extremely small and cannot be detected by even the most sensitive devices" with exact certainty but determined with facts. [Mass changed into energy should not be treated as an extreme mass.] Appreciate the ratio of mass lost to mass of zinc required for same amount of energy obtained.

Answer: $\boxed{3}$

The problem is befooling one. We have to just get energy per gram ratio for the cell Given. Actually the A joule divided by B gram denotes x joule per gram of zinc. I think all can evaluate that.its equal to emf*Faraday charge/ eqv mass.