A real HOTPO-tato

Number Theory Level 1

Define the operation "HOTPO" as follows, for positive integers.

If n is odd and greater than 1, form 3n+1

If n is even, form n/2

If n = 1, terminate the process

Example:

It takes 5 operations for HOTPO (5) to terminate.

HOTPO (5) = 16

HOTPO (16) = 8

HOTPO (8) = 4

HOTPO (4) = 2

HOTPO (2) = 1 (stop)

How many operations does it take for HOTPO(17) to terminate?


The answer is 12.

Denton Young by Denton Young , 47, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Denton Young
Aug 20, 2015

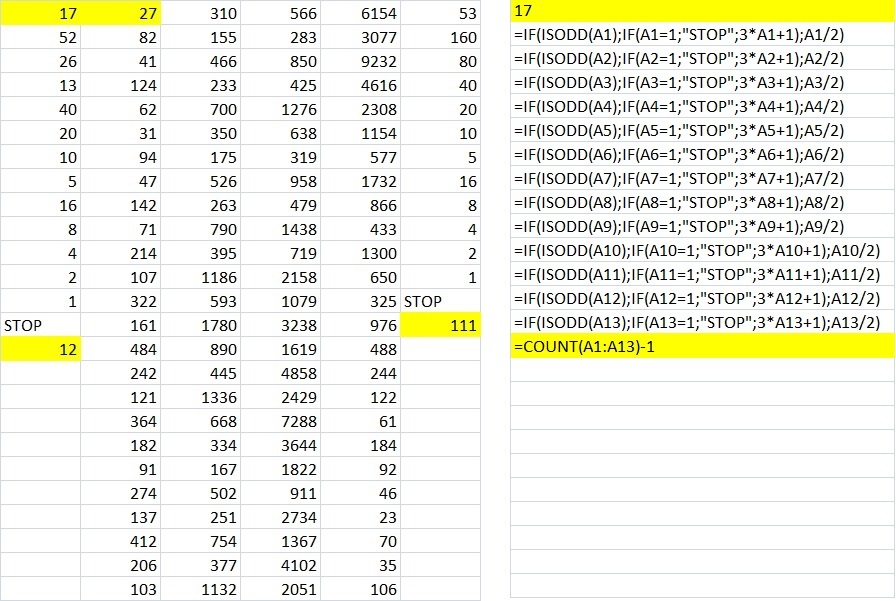
HOTPO (17) = 52

HOTPO (52) = 26

HOTPO (26) = 13

HOTPO (13) = 40

HOTPO (40) = 20

HOTPO (20) = 10

HOTPO (10) = 5

HOTPO (5) = 16

HOTPO (16) = 8

HOTPO (8) = 4

HOTPO (4) = 2

HOTPO ( 2) = 1 (stop)

Try tracking HOTPO (27). Bring a good-sized sheet of paper.

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Edwin Gray
Sep 8, 2018

We should have called the function Collatz, after Luther Collatz who first conjectured that the defined sequence will always terminate at 1.(1937). For those looking for something to do, it is still an open question. Ed Gray

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Chew-Seong Cheong
Aug 23, 2015

I have written an Excel spreadsheet to solve it. H O T P O ( 17 ) = 12 HOTPO(17)=12 and H O T P O ( 27 ) = 111 HOTPO(27) = 111 .

0 Helpful 0 Interesting 0 Brilliant 0 Confused 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
 
hotpo = 17

ctr = 0
while hotpo != 1:
    if hotpo % 2:
        hotpo = hotpo*3 + 1
        ctr += 1
    else:
        hotpo /= 2
        ctr += 1

print ctr

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...