A really weird problem
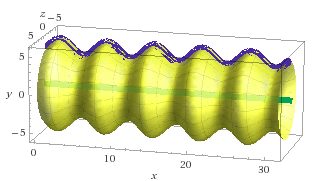
A tunnel is defined by revolved around the x-axis within the domain . Suddenly, the whole tunnel is filled completely with cement. Magic happens and only the cement cast is left. If , the volume of the cement cast in cubic units, can be represented in the form , where and are integers, find .
NB: Please evaluate the integral by hand, or you'll miss out on the fun!
The answer is 512.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of the circle at any point in the interval x ∈ [ 0 , 2 0 π ] is π [ f ( x ) ] 2 = π ( s i n x + 5 ) 2 . Since x varies from 0 to 2 0 π , the volume is given by V = ∫ 0 2 0 π π ( s i n x + 5 ) 2 d x = π ∫ 0 2 0 π s i n 2 x d x + 1 0 π ∫ 0 2 0 π s i n x d x + 2 5 π ∫ 0 2 0 π d x .
π ∫ 0 2 0 π s i n 2 x d x = 1 0 π 2
1 0 π ∫ 0 2 0 π s i n x d x = 0
2 5 π ∫ 0 2 0 π d x = 5 0 0 π 2
∴ V = 1 0 π 2 + 0 + 5 0 0 π 2 = 5 1 0 π 2
We conclude that a = 5 1 0 and b = 2 . Therefore:
a + b = 5 1 2