Rectangle And Triangle Inside Circle
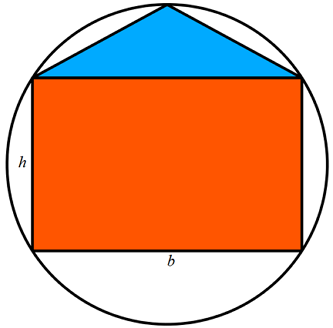
Inscribe a rectangle of base b and height h and an isosceles triangle of base b inside a circle of radius one as shown in the figure above.
The center of the circle coincides with the point of intersection of the diagonals of the rectangle.
For what value of h do the rectangle and triangle have the same area ?
The answer is 0.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The area of the rectangle, denoted by S 1 , is S 1 = h ∗ b . For the area of the triangle, denoted by S 2 , we can see that its base is of length b . As for its height, if we pass a line from the center of the circle to the top of the triangle we will have a radius of length R . Now, the length of the radius is the sum of the height of the triangle and half the height of the rectangle. Therefore the height of the triangle is R − 2 1 h . The area of the triangle is therefore S 2 = 2 b ( R − 2 1 h ) .
We want to have S 1 = S 2 : h ∗ b = 2 b ( R − 2 1 h ) .
We can remove b from both sides and multiply by 2
2 h = R − 2 1 h
2 . 5 h = R − − > h = 0 . 4 R .
In our case R = 1 therefore h = 0 . 4
Since the triangle and the rectangle have the same base = b, the height of the triangle has to be twice the height of the rectangle for their areas to be equal, by the formulas for areas: Area of rect = b h, Area of tri. = .5 b H, where H is the height of the triangle b h=.5b*H --> divide by b --> h = .5H --> multiply by 2 --> 2h=H
Looking at the diagram, if you draw a radius straight up from the center of the circle, you see that it's length is .5h to the top of the rectangle and another 2h to the edge of the circle = 2.5h total
The radius of the circle is 1, therefore 2.5h=1 --> 5h/2=1 --> h = 2/5 = .4
The area of triangle is given by:
A △ = 2 1 b h △ = 2 1 b ( 1 − 2 h ) = 4 b ( 2 − h ) where h △ is the height of the triangle. Note that 1 is the radius of the circle.
Now, the area of the rectangle A □ = b h . So for A △ = A □ , we have:
A △ 4 b ( 2 − h ) b ( 2 − h ) 2 − h 5 h ⟹ h = A □ − b h = 4 b h = 4 h = 2 = 5 2 = 0 . 4