A Rectangle inside a Triangle!
Given a Δ A B C with D E ∥ B C , with D ∈ A B and E ∈ A C . Drop perpendiculars from D and E to B C , meeting B C at F and K respectively.
If [ D E K F ] [ A B C ] = 7 3 2 , find the value of ∣ B D ∣ ∣ A D ∣ .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
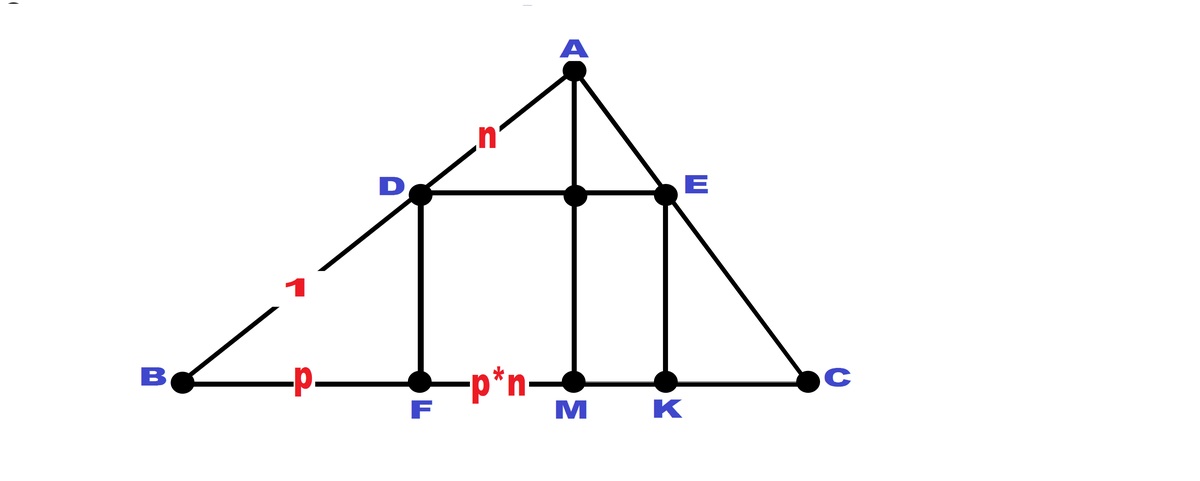 Let
A
M
⊥
B
C
. Let n=
D
B
A
D
. p=
A
B
B
C
.
Let
A
M
⊥
B
C
. Let n=
D
B
A
D
. p=
A
B
B
C
.
The proportions in the similar triangles, because of DE || BC and DF || AM are as under.
A
B
A
D
=
n
+
1
n
=
B
C
D
E
,
S
i
m
i
l
a
r
l
y
p
D
F
=
p
+
p
∗
n
A
M
.
∴
D
E
∗
D
F
=
{
B
C
∗
n
+
1
n
}
∗
{
A
M
∗
p
+
p
∗
n
p
}
=
(
n
+
1
)
2
n
∗
B
C
∗
A
M
⟹
2
∗
Δ
A
B
C
=
n
(
n
+
1
)
2
∗
D
E
K
F
⟹
2
n
(
n
+
1
)
2
=
7
3
2
(
g
i
v
e
n
)
C
l
e
a
r
l
y
D
B
A
D
=
n
=
7
Image from GeoGebra .
Let x = ∣ B D ∣ ∣ A D ∣
Let △ A D E have area y . Hence [ △ A B C ] = ( x x + 1 ) 2 y by property of similar triangles, since D E ∥ B C .
Now note that the total shaded area is 3 2 2 5 [ △ A B C ] = 3 2 2 5 ( x x + 1 ) 2 y .
When the two shaded triangles at the bottom, △ B D F and △ C E K , are joined, the resultant triangle is similar to △ A D E . Hence their total area is x 2 y .
Equating, y + x 2 y = 3 2 2 5 ( x x + 1 ) 2 y 1 + x 2 1 = 3 2 2 5 x 2 x 2 + 2 x + 1
Multiplying by 3 2 x 2 , 3 2 x 2 + 3 2 = 2 5 x 2 + 5 0 x + 2 5 7 x 2 − 5 0 x − 7 = 0 ( 7 x + 1 ) ( x − 7 ) = 0
Since x > 0 , we have x = 7