A rectangle's sides
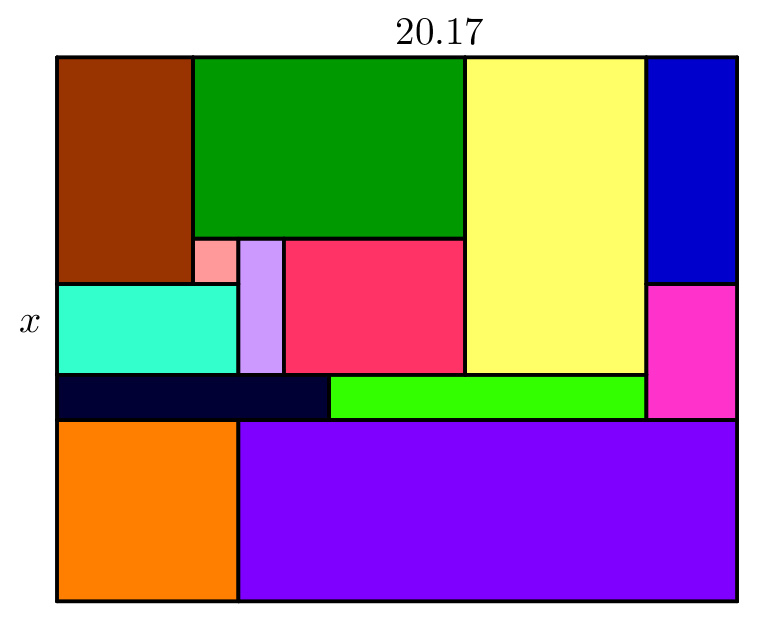
A rectangle is divided into smaller rectangles. Each small rectangle has at least one side which length is an integer. The big rectangle's sides are and . We know that , where is a non-negativ integer. What is the minimum value of ? (You can choose how you divide the rectangle, the figure is just an example.)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Place the rectangle into a chess board, where each small chess-square's side is 2 1 . Since each small rectangle has a side which lenght is an integer, every small rectangle covers the same area of balck and white. So the big rectangle covers the same area of black and white. If we prove that if a rectangle covers the same area of black and white, then it has a side which lenght is an integer, we get the answer is 2 0 1 7 = 0 . 2 0 1 7 ∗ 1 0 n . Suppose it is not possible. Cut the rectangle in the lower right corner of the big rectangle with sides long enough for the sides of the two sides to exceed the closest one. The concave hexagon covers the same are of black and white, so the area which was cutted, covers the same area of balck and white. But by calculating we can easily get, that this is impossible.
So the answer is n = 4 .
(It is easy to find a possible dividing.)