A Regular Polygon from Midpoints
This concave kite has a special property that when you join the midpoints of its adjacent sides, a square is formed such that one vertex of the concave kite is in the exact center of the square.
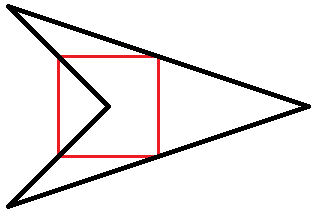
The kite and square above have sides. Give the number of sides of the next simple polygon for which it is possible to join the midpoints of its adjacent sides to form a regular polygon such that one vertex of the original polygon is in the exact center of the regular polygon. (In this question, a simple polygon is defined as being closed, not sharing more than one vertex with itself, and not self-intersecting.)
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
An easier approach is to start with a point at the center of a regular polygon, reflect the point across a vertex, then reflect that point across the next vertex, and so on, and finally drawing a line through each consecutive point. Although the coordinates for each polygon can be found exactly, quick sketches are sufficient to show that starting with a regular polygon with an odd number of sides do not join to make a closed simple polygon, and starting with a regular hexagon will result in a shape that shares a vertex in the center.
Starting with a regular octagon does produce a closed simple polygon, as shown above, and so n = 8 .