A resistors puzzle
In the figure below, all resistors have resistance
R
=
1
Ω
. Find the equivalent resistance
in Ohms
between the points A and O.
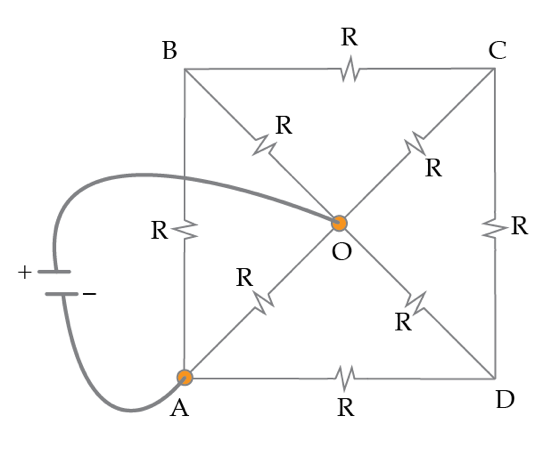
The answer is 0.47.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
We must first determine the direction of current flow for each of the segments in the circuit. It is easy to see that the current flows from O to A, from O to B, from O to C and from O to D. We can also see that the current flows from C to B, from C to D, from B to A and from D to A. Note that since the circuit is symmetric, we have:
(1) The current flowing from O to B is equal to that from O to D.
(2) The current flowing from C to B is equal to that from C to D.
(3) The current flowing from B to A is equal to that from D to A.
Suppose the emf of the electric supply is V volts and the total current flowing from O to A is I amperes. We can let the currents flowing from O to A, B and C be I 0 , I 1 and I 2 respectively. The current from O to D is thus also I 1 . At C, the current splits equally and flows to B and D, so the currents flowing from C to B and from C to D are both 2 1 I 2 . The current flowing from B to A (and hence from D to A as well) is the sum of the currents flowing from C to B and from O to B, so it is I 1 + 2 1 I 2 .
Now, we denote the resistor connecting any two points X and Y as resistor XY. Since the potential difference between O and A is V volts and a current of I 0 amperes flows through resistor OA, then I 0 = R V . Considering the potential difference across O and B, we see that the voltage across resistor OB is equal to the sum of the voltages across resistors OC and CB. Since the resistors all have the same resistance, we can divide this relation throughout by R to obtain I 1 = I 2 + 2 1 I 2 = 2 3 I 2 . In addition, the potential difference across O and A (which is V volts) is equal to the sum of the voltages across resistors OB and BA. This gives us the relation V = I 1 R + ( I 1 + 2 1 I 2 ) R = 2 7 I 2 R . Therefore, I 2 = 7 2 ⋅ R V and I 1 = 2 3 I 2 = 7 3 ⋅ R V .
We are now ready to solve the problem. The total current flowing from O to A, in amperes, is I = I 0 + 2 I 1 + I 2 = R V + 2 ⋅ 7 3 ⋅ R V + 7 2 ⋅ R V = 7 1 5 ⋅ R V . The potential difference between O and A is V volts. Therefore, the resistance between O and A is I V = 7 1 5 ⋅ R V V = 1 5 7 R . Since R = 1 ohm, then the resistance between O and A, in ohms, is 1 5 7 = 0 . 4 7 .
Assume you connect a battery between P and Q . A current I will start flowing through the circuit from P to Q. V = IR, R = V/I.
Denote :
POAQ : loop 1
ABO : loop 2
BCO : loop 3
I PO = I AQ = I
I DA = I BA = I_1
I OA = I 2
I OB = I OD = I_3
I OC = I 4
I CB = I CD = I_5
For the junction at point A we have 2 I 1 + I 2 - I = 0
For the junction at point O we have I 2 + 2 I 3 + I_4 - I = 0
For the junction at point B we have I 1 - I 3 - I_5 = 0
For the junction at point C we have I 4 - 2 I 5 = 0
For loop 1 we have V - 1*I_2 = 0
For loop 2 we have 1 I_2 - 1 I 1 - 1*I 3 = 0
For loop 3 we have 1 I_3 - 1 I 4 - 1*I 5 = 0
Work out all the equations above , we get :
I 2 = (7/4) I 1
2 I 1 + I 2 - I = 0
2 I 1 +(7/4) I 1 - I = 0
I = (15/4) I_1
V - 1*I_2 = 0
V = (7/4) I_1
R = V / I
R = ( (7/4) I 1 ) / ( (15/4) I 1 )
R = 7/15
R = 0.47
Let the potential difference between O and A be V. We will consider that the current flows from A to O as the effective resistance is independent of the direction of current.
Let current i enter through A.
By symmetry, the current splits up as i 1 , ( i − i 1 ) / 2 and ( i − i 1 ) / 2 through AO, AB and AD respectively.
At B, the current again splits as i 2 and ( i − i 1 ) / 2 − i 2 through BO and BC respectively. Similarly, at D, the current splits as i 2 and ( i − i 1 ) / 2 − i 2 through DO and DC respectively.
At C, the current combines and passes through CO as i − i 1 − 2 i 2 .
So, if the effective resistance is R e q , the equations are:
R V = i 1 -----(1) [Considering path AO]
R V = ( i − i 1 ) / 2 + i 2 -----(2) [Considering path AD and DO]
R V = ( ( i − i 1 ) / 2 ) + ( ( i − i 1 ) / 2 − i 2 ) + ( i − i 1 − 2 i 2 ) = 2 i − 2 i 1 − 3 i 2 -----(3) [Considering path AD, DC and CO]
Comparing (1) and (2), i 1 = ( i − i 1 ) / 2 + i 2 or, 3 i 1 = i + 2 i 2 ------------(4)
Comparing (1) and (3), i 1 = 2 i − 2 i 1 − 3 i 2 or, 3 i 1 = 2 i − 3 i 2 -------------(5)
Solving (4) and (5), we get i 1 = 1 5 7 i . Putting this in (1), we get R V = 1 5 7 i or, R e q = i v = 1 5 7 R = 0 . 4 6 7 o h m (with R=1 ohm)
The challenge to traditional resistor simplification is the upper-right corner, which is neither in series nor in parallel with the rest of the circuit.
To address this*, recognize that the current that would be flowing from O to C will then be split equally - going to B or D next. So we can replace the OC resistor with two separate resistors - each with double resistance (2 \Ohm ). These new resistors are respectively in series with the CB and CD resistors - now giving us two symmetrical legs of the circuit that are in parallel.
Considering each leg separately at first (say, the lower right leg), we have a 2 \Ohm resistor in series with a 1 \Ohm (CD). These sum to 3 \Ohm.
Now we have a 3 \Ohm resistor in parallel with the OD resistor. Using \frac{1}{R_eq.} = \frac{1}{3 \Ohm} + \frac{1}{1 \Ohm}, we get equivalent resistance of \frac{3}{4} \Ohm.
This is now in series with resistor AD for a sum of 1.75 \Ohm.
We repeat this for the symmetrical leg, taking care of CB, OB, and BA. This again yields 1.75 \Ohm.
Finally, we find the equivalent resistance of the two legs and the OA resistor: \frac{1}{R_eq.} = \frac{1}{1.75 \Ohm} + \frac{1}{1 \Ohm} + \frac{1}{1.75 \Ohm} = 0.466 \ldots, which rounds to 0.47.
- Another way to think about this is to slice the OC wire and resistor down the middle, letting each side then connect to the CB or CD resistors next.
In the given figure , the points B and D are the same by symmetry .
So we rename both the points as D .
Thus on simplifying the given figure we get the following figure :
By further working on the resistance between D and C and then subsequently between O and D and finally between O and A .
We get 2 R , 2 8 R and 1 5 7 R respectively .
Since : R = 1 ,
We get :
R n e t = 1 5 7 = 0 . 4 6 ˉ ≈ 0 . 4 6 7