A Rigid Problem About A Rigid Hoop
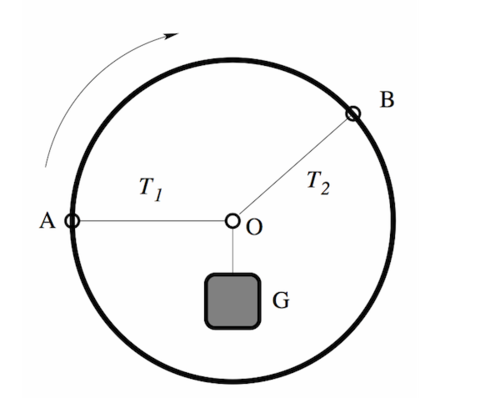A rigid hoop can rotate about the center. Two massless strings are attached to the hoop, one at
A
, the other at
B
. These strings are tied together at the center of the hoop at
O
, and a weight
G
is suspended from that point. The strings have a fixed length, regardless of the tension, and the weight
G
is only supported by the strings. Originally
O
A
is horizontal.
Now, the outer hoop will start to slowly rotate 9 0 ∘ clockwise until O A will become vertical, while keeping the angle between the strings constant and keeping the object static. Which of the following statements about the tensions T 1 and T 2 in the two strings is correct?
Note : This problem appeared on the 2012 F = ma exam.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
talk about T1 dude it is always increasing in this problem which is also an option
Log in to reply
Hmm yeah I should have mentioned that.
Looking at the initial diagram: Find the sum of the forces in the Y direction. I will set up and to the right as positive. If θ is the acute angle between T2 and the horizontal, then the sum is
T 2 sin θ − m g = 0
T 2 sin θ = m g
T 2 = sin θ m g
Find the sum in the X direction:
T 2 cos θ − T 1 = 0
T 1 = T 2 cos θ
Plug in T2:
T 1 = ( sin θ m g ) × cos θ
T 1 = m g × cot θ
Looking at the Y direction in the end diagram:
T 1 − T 2 cos θ − m g = 0
T 1 = T 2 cos θ + m g
However, we know that T2 in the end is zero (what I explained in my solution). So,
T 1 = m g
This shows that the initial T1 is cot θ times greater than the final T1. But in cot θ can be greater than or less than 1. (Greater than if θ > 4 5 ∘ , less than if θ < 4 5 ∘ . So depending on θ , T1 could be increasing or decreasing.
Log in to reply
Wow yar fantastic reply,you're a genius indeed.Keep your wits about you,I am your fan...
God!! Hey even T1 always increases... Why isn't that correct?
Hey why have you taken minus sign between T1 and T2cos theta of end diagram in the reply below,you know because they act in the same direction,so intead they shoud up and support the weight aint it
Log in to reply
They actually point in opposite directions. See how in the initial diagram T1 and the x-component of T2 are in opposite directions? It's the same thing in the end diagram, just rotated 90 degrees.
okay i am sorry,i was wrong, my bad and my mistake i was considering the initial
diagram for the end equations in the Y direction
Very interesting problem
yea! even i solved it d same way! :)
when sting becomes vertical then tension in string becomes mg in other becomes zero
T1 directly hold the weight, because the position after rotation T2 is below of G, so T2 not holding any weight . instead if the string at T2 have a mass, it will increase the T1
First, draw a force diagram of the forces at point O when the hoop is in the initial position. I can't draw a diagram, but it 3 forces should be present: T1 pointing directly to the left, T2 pointing diagonally upwards and to the right, and the weight of G pointing downwards.
Next, draw the diagram for the end of the rotation. Now T1 is pointing up, the T2 is diagonally downwards and to the right, and the weight of G is still straight down.
The system is in static equilibrium at the end of the rotation, so there should be no net force. T2 has an x-component pointing to the right, but there is no other force with an x-component pointing to the left to cancel T2 out. Therefore, the force of T2 must be zero at the end of the rotation.