A ring in a magnetic field

Electricity and Magnetism Level 3

A conducting ring of radius R = 10 m R=10 m is placed in a homogeneous magnetic field, perpendicular to its plane. A constant current I = 0.1 A I=0.1 A flows through the ring. It is known that the ring breaks if its tension is greater than 5N. What is the maximum magnetic field B m a x B_{max} in Teslas that one can apply without breaking the ring? Neglect the magnetic field created by the current in the ring.


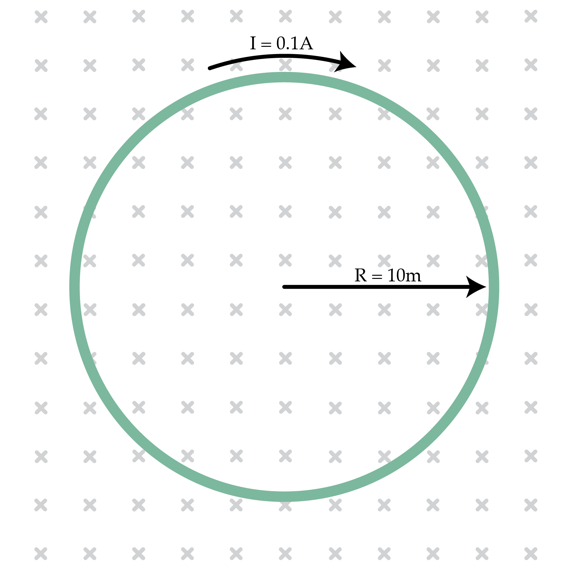
The answer is 5.

David Mattingly by David Mattingly

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Mattingly Staff
May 13, 2014

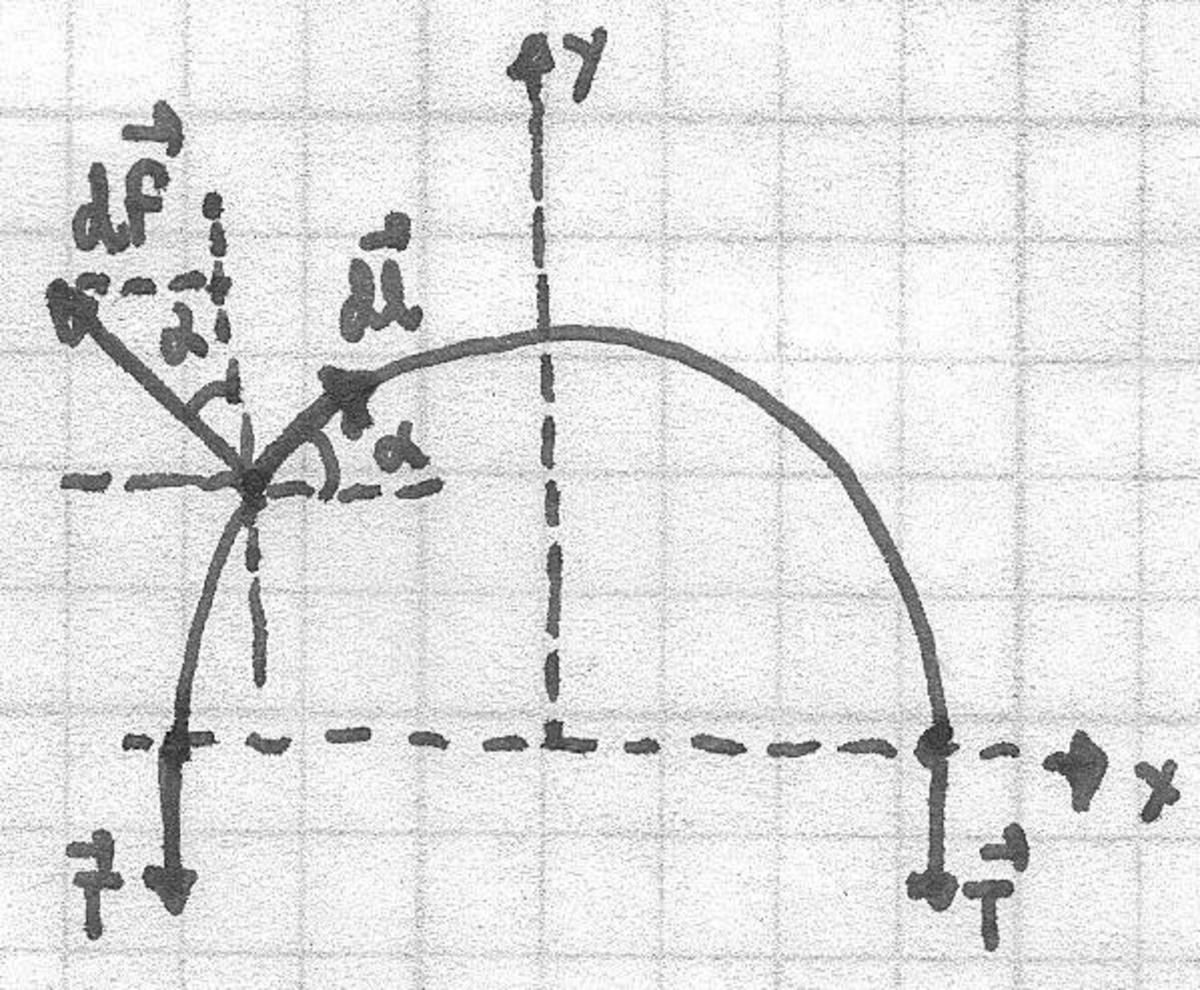
Let us consider focus on one half of the ring. The magnetic force acting on an element d l dl is given by d F = I d l B dF= I dl B From symmetry it is clear that the total magnetic force will be directed along the y-axis (we choose the y axis to be perpendicular to the diameter) Denoting the tension in the ring by T, we can write 2 T = ∫ d F y = ∫ d F c o s ( α ) = I B ∫ d l cos ⁡ ( α ) = I B ∫ d l x = I B ( 2 R ) . 2 T= \int dF_{y}= \int dF cos(\alpha) = IB \int dl\cos(\alpha)= I B \int {dl}_{x}= I B (2 R). From this equation, we conclude that B m a x = T m a x I R = 5 T e s l a s . B_{max}= \frac{T_{max}}{I R}= 5 Teslas.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...