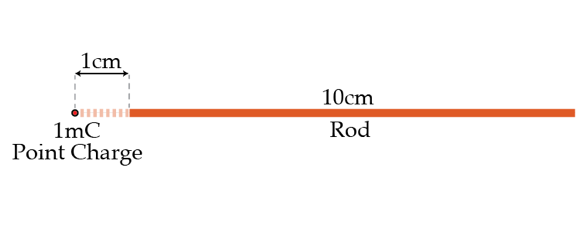
A rod near a point charge

The net force on the rod is given by an integral of the forces on infinitesimal sections of the rod, i.e.

$F=\int_0^L kq \frac{\lambda dx}{(L+d-x)^2}$

where $L$ is the length of the rod, $d$ is the distance the point charge is from the rod, $q$ is the magnitude of the point charge, and $\lambda$ is the linear charge density on the rod. We can explicitly evaluate this integral to get

$F=\frac{kqL\lambda }{(L+d)d}=\frac{kqQ}{(L+d)d}$

where $Q$ is the total charge of the rod. We can then solve this for $Q=1.22~\mbox{nC}$ .