A romantic evening of physics
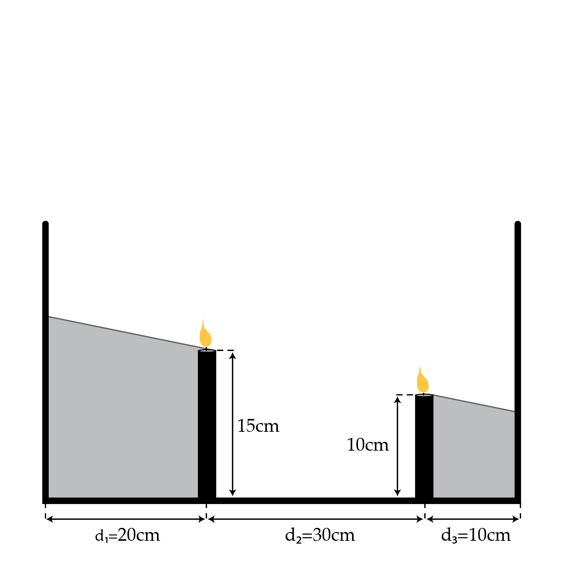
Two candles are placed on a table between two parallel walls that are perpendicular to the ground. The line that passes through the bottom of these candles (which are on the ground) is also perpendicular to the walls.
These two candles separate the space between the walls into three regions of length d 1 = 2 0 cm , d 2 = 3 0 cm , d 3 = 1 0 cm (from the left to right).
The candle on the left is Candle 1, and the other is Candle 2. The height of Candle 1 is h 1 = 1 5 cm and Candle 2 is h 2 = 1 0 cm .
Now light these candles - their height shrinks with time. The rate at which Candle 1's height shrinks is 2 times faster than Candle 2's rate.
The question:
On the left wall, we see the shadow of Candle 1; on the right wall we see the shadow of Candle 2. Find the ratio of the speed of the Candle 1 shadow's top to Candle 2 shadow's top.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Excellent........
Superb
forgive me .... as English is not my native tongue ...............what does "Top to" means ?... can someone simplify this problem....
Log in to reply
they are basically asking the ratio of
s p e e d o f C 2 ′ s s h a d o w ′ s t o p s p e e d o f C 1 ′ s s h a d o w ′ s t o p
top means peak of the candle
gj
1) Solve what would be the height of Shadow 1 (shadow of candle 1 on the left wall) and Shadow 2 (shadow of candle 2 on the right wall) at the given conditions.
Let
x = height of shadow of candle 1
y = height of shadow of candle 2
A = angle included between the wall on the left and the line from the tip of candle 1 to the tip of its shadow on the left.
G = distance from the bottom of the wall on the right to the tip of the constructed triangle. (Construct a triangle from the path of the ground and the shadow on the right of the wall)
Then
A = arctan (30/5) -- from the constructed triangle b/n the candles due to height difference
A = 80.53767779
tan (90-A) = 10 / (10 + G)
Solving for G, G = 50
tan (90-A) = x / 110 -- >110 = 20 + 30 + 10 +70
x = 55/3
tan (90-A) = y / 50
y = 25/3
2) Assume a change in height of 2 cm on candle 2 in 1 hr. Then candle 1 would've shrink 4 cm since the ratio of shrink rate b/n candle 1 and 2 is 2. Then the new height of candle 1 = 15 - 4 = 11 cm and candle 2 = 10 - 2 = 8 cm.
Now, a new triangle.
Let
x' = new height of the shadow of candle 1
y' = new height of the shadow of candle 2
A' = new angle included
G' = new distance from bottom of wall on the right to the vertex of the constructed triangle.
Then
A' = arctan (30/3)
tan (90-A') = 8 / (10 +G')
G' = 70
tan (90-A') = x' / (60 + 70)
x' = 13
tan (90-A') = y' / 70
y' = 7
Delta x = (55/3) - 13
Delta y = (25/3) - 7
ratio = Delta x / Delta y
ratio = 4 --> Ans.
Let the length's of Candle 1, Candle 2 and their respective shadows be x , y , h 1 & h 2 respectively. Then from similarity we can say
h 2 − x h 2 − y = 4 1 ----- ( i )
h 2 − h 1 h 2 − x = 3 2 ----- ( i i )
Differentiating both sides of ( i ) and ( i i ) w.r.t ' t ' and setting d t d ( x ) = 2 ⋅ d t d ( y ) , we get
d t d ( h 1 ) = 4 ⋅ d t d ( h 2 ) .
So our desired answer is 4 .
Let the heights of shadows of Candle 1 and Candle 2 be s 1 and s 2 respectively.
Also, we construct a straight line joining the top of the 2 shadows and the 2 candles. Horizontal lines from the top of Candles 1 and 2 and shadow 2 to each vertical to the left respectively are also constructed.
From the problem statement, we know that d t d h 1 = 2 ⋅ d t d h 2 . This means that d h 2 d h 1 = 2 .
Now we consider the triangles constructed. The angle of the slanted line with the verticals is constant. So we have similar triangles.
From there, we obtain d 2 h 1 − h 2 = d 1 s 1 − h 1 . Substituting values gives s 1 = 3 5 h 1 − 2 h 2 .
We can also obtain d 2 h 1 − h 2 = d 3 h 2 − s 2 . Another substitution yields s 2 = 3 4 h 2 − h 1 .
We perform implicit differentiation on both equations.
-
Differentiating s 1 = 3 5 h 1 − 2 h 2 gives 3 ∗ d h 2 d s 1 = 5 d h 2 d h 1 − 2 .
-
Differentiating s 2 = 3 4 h 2 − h 1 yields 3 ∗ d h 2 d s 2 = 4 − d h 2 d h 1
Dividing equation 1 with equation 2 gives d s 2 d s 1 = 4 − d h 2 d h 1 5 d h 2 d h 1 − 2 .
Substituting d h 2 d h 1 = 2 yields d s 2 d s 1 = 4 .
Assuming that the shadow of one candle is only created due to the other candle
Set up the x-y coordinate system where the top of Candle 1 is at (20, 15) and Candle 2 at (30,10). Easily seen that the top of the shadows is the intersection between the line passing through these two points and the line x =0 and x = 60.
This line has the equation:
y = f ( x ) = m x + c
The ratio asked in the question is simply f(0)'/f(60)'.
f ( 0 ) ′ = d t d m ∗ 0 + d t d c
f ( 6 0 ) ′ = d t d m ∗ 6 0 + d t d c
So the problem now is to calculate dm/dt and dc/dt
We know that
m = 2 0 − 5 0 f ( 2 0 ) − f ( 5 0 )
Let 2a be he rate of decreasing of candle 1, thus a is the rate of decreasing of candle 2.
Hence,
d t d m = 2 0 − 5 0 f ( 2 0 ) ′ − f ( 5 0 ) ′ = − 3 0 a
We also have: f ( 2 0 ) ′ = d t d m ∗ 2 0 + d t d c = 2 a
→ d t d c = 3 8 a
Using those value plug in
f ( 6 0 ) ′ f ( 0 ) ′ = − 2 a + 3 8 a 3 8 a = 4
The line joining the peaks of the candles will intersect the wall,say L1 for left wall & R1 for right wall. So if the speed of shadow of C1 is V1 then V1=
t 1 − 0 ( H e i g h t o f S h a d o w o f C 1 a t t = t 1 − h e i g h t a t t = 0 )
Similarly, the speed of shadow of C2 is V2 then V2=
t 1 − 0 ( H e i g h t o f S h a d o w o f C 2 a t t = t 1 − h e i g h t a t t = 0 )
We need to find V 2 V 1 . Initially the length of the shadow on the left wall is (10+25/3)cm, and on the right wall is (10-5/3)cm. Now the candle C1 burns at twice the rate of C2, so for after t unit time , height of shadow of C1 on left wall=15-2x height of shadow of C2 on right wall=10-x
When height of shadow on the left wall is 0, we will get similar triangles, where 2 0 1 5 − 2 x = 5 0 1 0 − x x= 8 5 5 therefore, 15-2x=15-2 8 5 5 = 4 5 Now, taking the height of shadow on the right wall as y, and similar triangles ratio 2 0 5 / 4 = 6 0 y
solving, y= 4 1 5
therefore, V 2 V 1 = ( 1 0 − 5 / 3 ) − 1 5 / 4 ( 1 0 + 2 5 / 3 ) − 0
The time component is same for both the numerator & denominator and will be cancelled.
Solving we get V 2 V 1 = 4
You should wrap up only math inside () . Alternatively give \, between words.
thanks bro!!
Set up a coordinate system. Candle 1's height is ( 2 0 , 1 5 − 2 v t ) and candle 2's height is ( 5 0 , 1 0 − v t ) . The intersection of the line connecting those two points with the walls are where the shadows will be.
We eventually find that this line has equation y = 3 0 − 5 + v t x + 3 5 5 − 8 v t
We plug in x = 0 and see that candle 1's shadow moves at speed 3 8 v . We then plug in x = 6 0 and work out the algebra and see that candle 2's shadow moves at speed 3 2 v . Next, we divide the two and end up with 4 .