A rose by any other name

Calculus Level 4

The collection of polar graphs, $r(t) = \cos(nt)$ , is a family of images of flowers (roses) of $n$ or $2n$ petals depending on $n$ being even or odd.

Out of the options given , which rose with that number of non-overlapping petals would have the greatest total area?

Image Credit: Flickr David Gilson .

5 7 9 6 8

2 solutions

Michael Mendrin
Aug 17, 2015

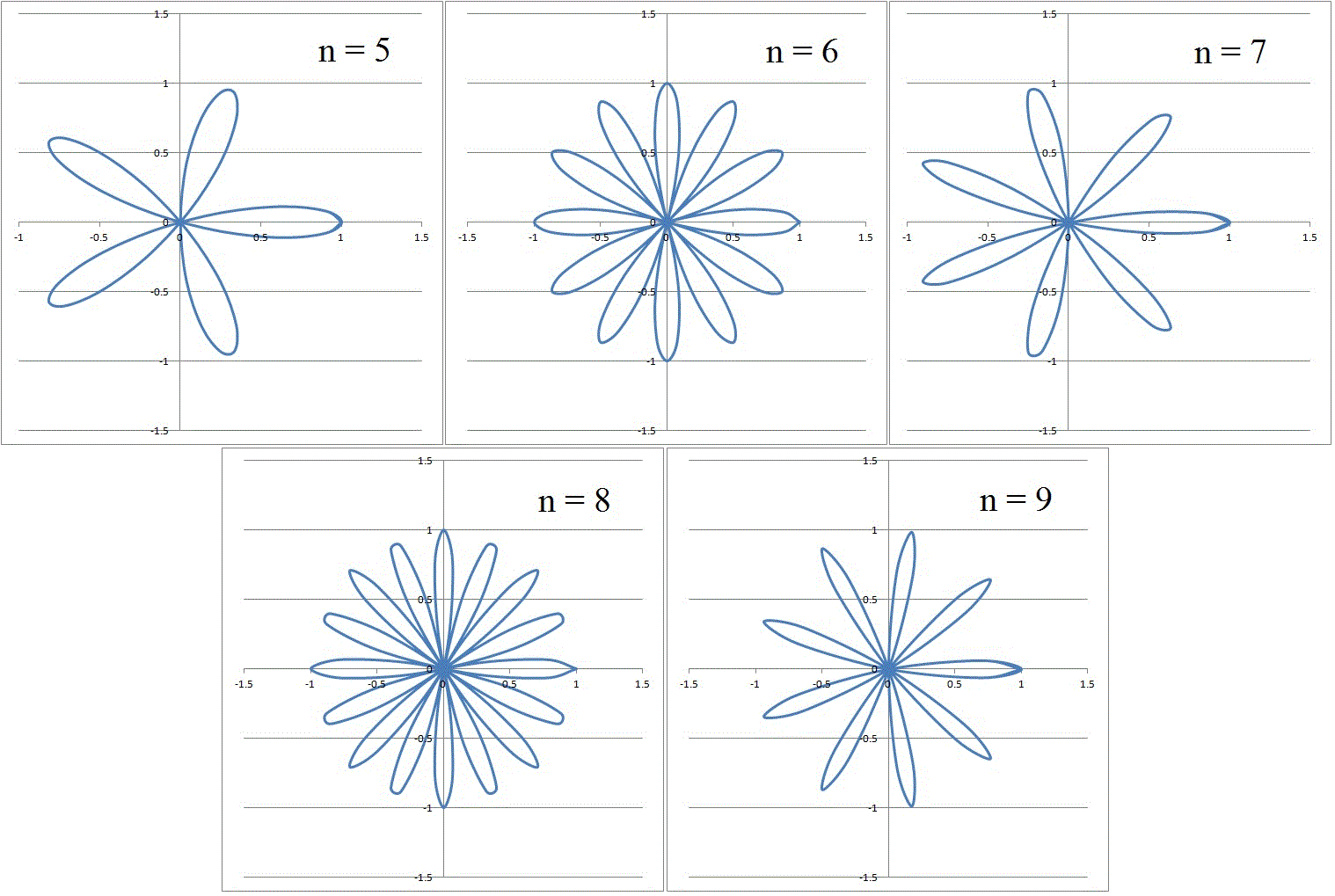
Very interesting problem!

We can integrate the polar equation for the area of exactly one petal, as follows

$\displaystyle \int _{ -\dfrac { \pi }{ 2n } }^{ \dfrac { \pi }{ 2n } }{ \dfrac { 1 }{ 2 } { \left( Cos\left( nt \right) \right) }^{ 2 } } dt=\dfrac { \pi }{ 4n }$

so that if there are $n$ petals, the total area is $\dfrac { \pi }{ 4 }$ , and if there are $2n$ petals, it's $\dfrac { \pi }{ 2 }$ . Hence, for the number of petals given as choices $5, 6, 7, 8, 9$ , we should look at $6$ and $8$ as candidates. However, the $6$ petal version, requiring that $n=\dfrac{3}{2}$ , overlaps, which makes moot its total area. Ergo, the answer is $8$ . Here are the $6$ and $8$ rose petal curves

Chew-Seong Cheong
Aug 19, 2015

I actually plotted out the roses to compare. There are no overlapping petals. I hope my graphs are correct. According to the graphs, $n=\boxed{8}$ with $16$ petals has the greatest petal area.

Moderator note:

Note that the options should correspond to "number of petals", instead of $n$ given in the question.

The number of petals shown would then be 5, 12, 7, 16, 9. The confusion over this problem is that it asks for the number of petals that has the greatest total area, given 5, 6, 7, 8, 9.

Try plotting a rose petal curve that has 6 petals, without plotting two separate rose petal curves and pasting them together.

Michael Mendrin - 5 years, 9 months ago

A rose by any other name

Image Credit: Flickr David Gilson .

2 solutions

Moderator note:

0 pending reports