A second order RC circuit frequency response
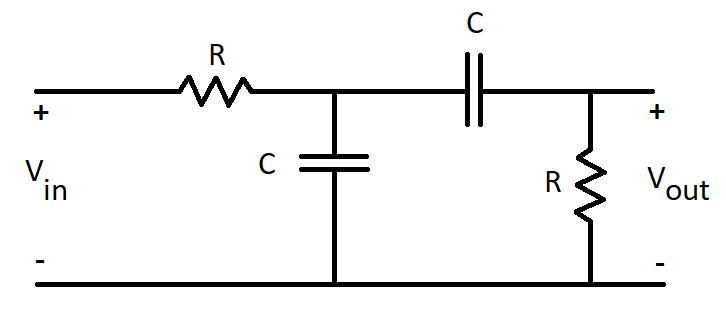
The above figure shows a circuit made with two identical resistors, R = 1 k Ω and two identical capacitors C = 1 μ F . The input voltage is V i n = A cos ω t V . Find the value of ω (in rad/sec) at which the amplitude of the output voltage V o u t is maximum, for a given fixed input amplitude A .
The answer is 1000.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great analysis. Thanks for sharing it.
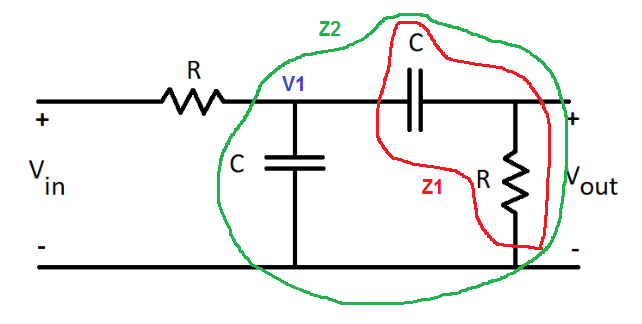
Let Z 1 = j ω C 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ( R + j ω C 1 ) , the C-C-R π circuit on the right. Then the impedance of the whole RC circuit is Z = R + Z 1 . And we have:
V i n V o u t = Z Z 1 × R + j ω C 1 R = R + Z 1 Z 1 × 1 + j ω C R j ω C R = R + 2 j ω C R − ω 2 C 2 R 1 + j ω C R 2 j ω C R − ω 2 C 2 R 1 + j ω C R × 1 + j ω C R j ω C R = 1 − ω 2 C 2 R 2 + j ω C R ( 1 + 2 R ) 1 + j ω C R × 1 + j ω C R j ω C R = 1 + 2 R + j ( ω C R − ω C R 1 ) 1 See note: Z 1 = 2 j ω C R − ω 2 C 2 R 1 + j ω C R
For the same ∣ V i n ∣ , ∣ V o u t ∣ is maximum , when ∣ ∣ ∣ ∣ 1 + 2 R + j ( ω C R − ω C R 1 ) ∣ ∣ ∣ ∣ is minimum or
ω C R − ω C R 1 ω 2 C 2 R 2 ω C R ⟹ ω = 0 = 1 = 1 = C R 1 = 1 0 − 6 × 1 0 3 1 = 1 0 0 0 rad/s
Note:
Z 1 = j ω C 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ( R + j ω C 1 ) = j ω C 1 + R + j ω C 1 j ω C 1 ( R + j ω C 1 ) = 2 j ω C R − ω 2 C 2 R 1 + j ω C R
Excellent analysis. Thanks for sharing this explanation.
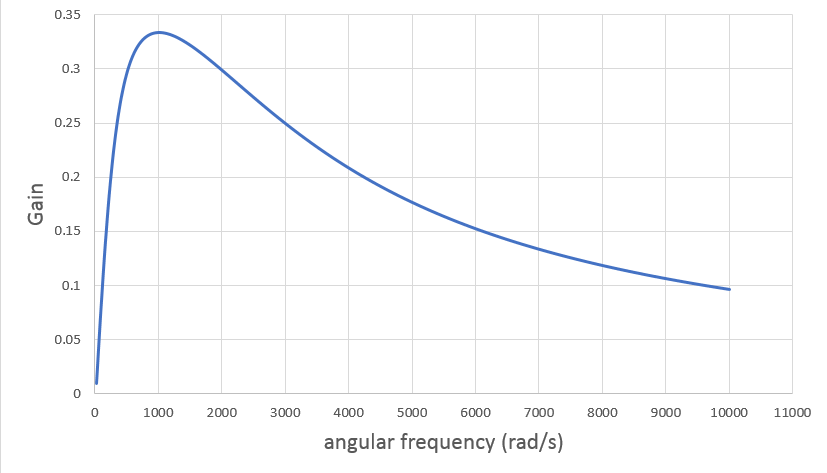
Sweep over the angular frequency and plot the gain at each value of ω .
Z C = − ω C j Z 1 = R + Z C Z 2 = Z 1 + Z C Z 1 Z C V 1 = V i n R + Z 2 Z 2 V o u t = V 1 R + Z C R Gain = ∣ ∣ ∣ V i n V o u t ∣ ∣ ∣
The gain has a maximum value of 3 1 at ω = 1 0 0 0 rad/s . This is not really a low-pass filter since it rejects DC. I will therefore call it a band-pass filter.
A great solution. Thanks for sharing it.
You're welcome, and thanks for the problem. May I use the graphic for a followup problem?
Absolutely.
Not an expert at Latex, neither am one in circuit analysis. My approach involves the use of the concept of transfer functions.