A short problem.
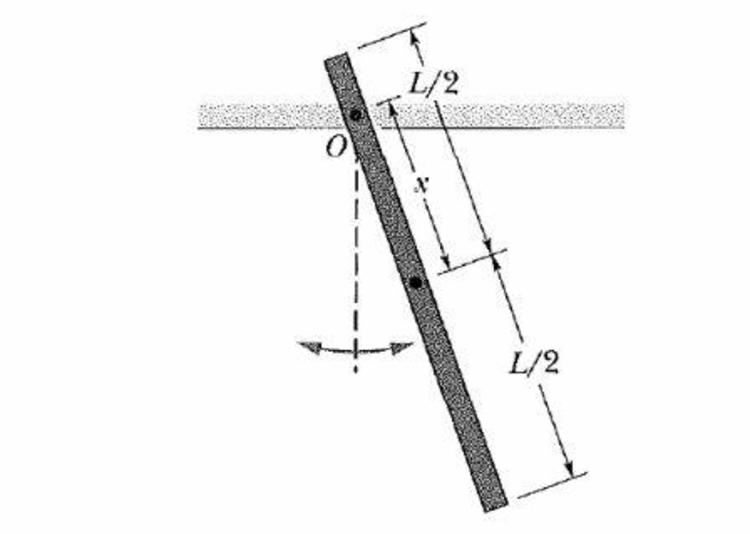 In the figure a stick of length
oscillates as a
physical pendulum.What value of distance (in
)
between the
stick's centre of mass and its pivot point
gives the least period
In the figure a stick of length
oscillates as a
physical pendulum.What value of distance (in
)
between the
stick's centre of mass and its pivot point
gives the least period
Liked it? Try more here
The answer is 0.53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Total torque acting on the rod about pivot must be equal to I p α .
⟹ m g x s i n θ = I p α
Since this is a restoring torque so − m g x s i n θ = I p α
⟹ α = I p − m g x s i n θ
Since for very small angular displacment s i n θ ≈ θ
So, α = I p − m g x θ
This is an equation of SHM whose angular frequency w = I p m g x
Therefore its time period T = w 2 π = 2 π m g x I p
= 2 π m g x 1 2 m L 2 + m x 2
= 2 π 1 2 g x L 2 + g x
Since A.M. is greater than or equal to G.M. and equality holds if and only if all the terms are equal. So for time period to be minimum 1 2 g x L 2 = g x
⟹ x = 2 3 L ≈ 0 . 5 3 m