Simple Similarity
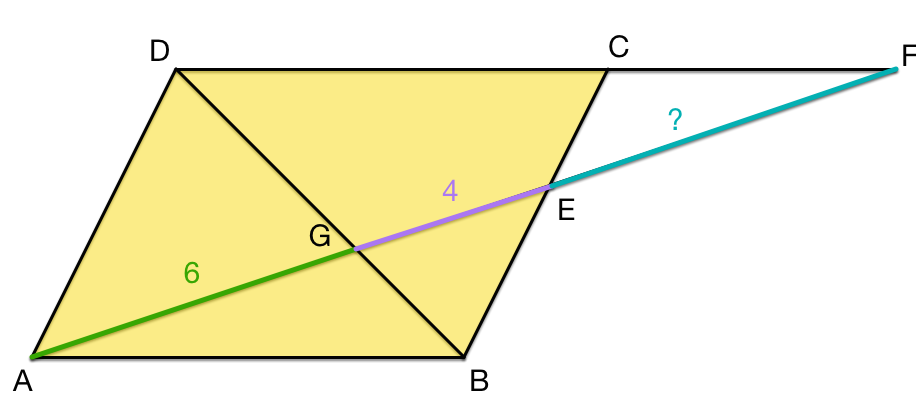
A B C D is a parallelogram. The point E is in the segment B C , and F is a point in the line D C such that A F pass through the point E and intersect the segment B D in the point G . If A G = 6 and G E = 4 . How long is E F ?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Moderator note:
Great observation with the similar triangles to simplify the work :)
After do with A B as a long side, and yes, the solution is more simple with this construction that is that you write
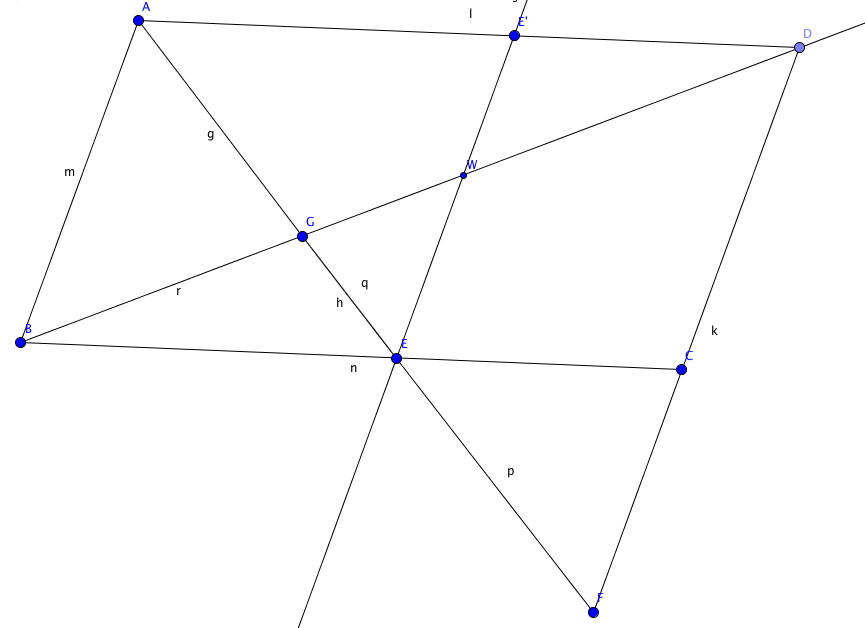 Draw the projection of
E
′
of
E
in the segment
A
D
and the segment
E
E
′
and intersect to
B
D
in
W
. Then
△
A
B
G
∼
△
G
E
W
∼
△
G
D
F
and
△
A
B
E
∼
△
E
C
F
then
G
E
A
G
=
4
6
=
E
W
A
B
therefore
E
W
=
3
2
A
B
.
If
C
F
=
k
then
D
F
=
A
B
+
k
and
E
W
D
F
=
2
A
B
3
(
A
B
+
k
)
. But as
△
G
E
W
∼
△
G
D
F
then
E
W
D
F
=
4
4
+
E
F
, therefore
2
A
B
3
(
A
B
+
k
)
=
4
4
+
E
F
then
6
(
A
B
+
k
)
=
A
B
(
4
+
E
F
)
⟹
6
A
B
+
6
k
=
4
A
B
+
E
F
⋅
A
B
⟹
2
A
B
=
E
F
⋅
A
B
−
6
k
. Given that
1
0
E
F
=
A
B
k
⟹
E
F
⋅
A
B
=
1
0
k
and substituting it in
2
A
B
=
E
F
⋅
A
B
−
6
k
therefore
2
A
B
=
1
0
k
−
6
k
=
4
k
∴
A
B
=
2
K
. Then
k
A
B
=
E
F
1
0
=
2
⟹
E
F
=
5
Draw the projection of
E
′
of
E
in the segment
A
D
and the segment
E
E
′
and intersect to
B
D
in
W
. Then
△
A
B
G
∼
△
G
E
W
∼
△
G
D
F
and
△
A
B
E
∼
△
E
C
F
then
G
E
A
G
=
4
6
=
E
W
A
B
therefore
E
W
=
3
2
A
B
.
If
C
F
=
k
then
D
F
=
A
B
+
k
and
E
W
D
F
=
2
A
B
3
(
A
B
+
k
)
. But as
△
G
E
W
∼
△
G
D
F
then
E
W
D
F
=
4
4
+
E
F
, therefore
2
A
B
3
(
A
B
+
k
)
=
4
4
+
E
F
then
6
(
A
B
+
k
)
=
A
B
(
4
+
E
F
)
⟹
6
A
B
+
6
k
=
4
A
B
+
E
F
⋅
A
B
⟹
2
A
B
=
E
F
⋅
A
B
−
6
k
. Given that
1
0
E
F
=
A
B
k
⟹
E
F
⋅
A
B
=
1
0
k
and substituting it in
2
A
B
=
E
F
⋅
A
B
−
6
k
therefore
2
A
B
=
1
0
k
−
6
k
=
4
k
∴
A
B
=
2
K
. Then
k
A
B
=
E
F
1
0
=
2
⟹
E
F
=
5
Well, maybe not that many auxiliary constructions are required.