A simple calculation
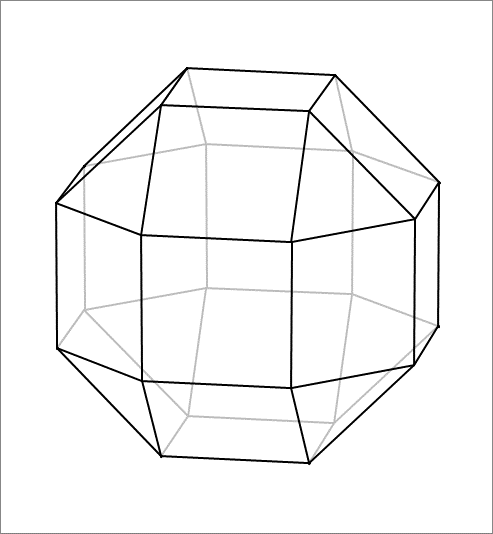
The figure above depicts a rhombicuboctahedron (also called small rhombicuboctahedron). All its faces are squares and equilateral triangles of the same edge length. If the edge length is find its volume. The volume can expressed as for positive integers with coprime. Enter .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To make a rhombicuboctahedron with unit sides, start with a unit cube, and on each its 6 faces attach a 1 × 1 × 2 2 box, and along each of its 1 2 edges attach a triangular prism with a height of 1 and legs of 2 2 , and along each of its 8 vertices attach a right tetrahedron with legs of 2 2 . The volume is then:
V rhomb = V cube + 6 ⋅ V box + 1 2 ⋅ V prism + 8 ⋅ V tetra = 1 3 + 6 ⋅ 1 ⋅ 1 ⋅ 2 2 + 1 2 ⋅ 2 1 ⋅ ( 2 2 ) 2 ⋅ 1 + 8 ⋅ 6 1 ⋅ ( 2 2 ) 3 = 4 + 3 1 0 3
Therefore, a = 4 , b = 1 0 , c = 3 , and a + b + c = 1 7 .